为减少烟尘排放对空气的污染，某同学设计了一个如图所示的静电除尘器，该除尘器的上下底面是边长为L＝0.20m的正方形金属板，前后面是绝缘的透明有机玻璃，左右面是高h＝0.10m的通道口。使用时底面水平放置，两金属板连接到U＝2000V的高压电源两极（下板接负极），于是在两金属板间产生一个匀强电场（忽略边缘效应）。均匀分布的带电烟尘颗粒以v=10m/s的水平速度从左向右通过除尘器，已知每个颗粒带电荷量 q＝+2.0×10－17C，质量m＝1.0×10－15kg，不考虑烟尘颗粒之间的相互作用和空气阻力，并忽略烟尘颗粒所受重力。在闭合开关后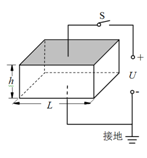
（1）求烟尘颗粒在通道内运动时加速度的大小和方向；
（2）求除尘过程中烟尘颗粒在竖直方向所能偏转的最大距离；
（3）除尘效率是衡量除尘器性能的一个重要参数。除尘效率是指一段时间内被吸附的烟尘颗粒数量与进入除尘器烟尘颗粒总量的比值。试求在上述情况下该除尘器的除尘效率；若用该除尘器对上述比荷的颗粒进行除尘，试通过分析给出在保持除尘器通道大小不变的前提下，提高其除尘效率的方法。
如图所示，足够长、宽度L1＝0.1m、方向向左的有界匀强电场场强E＝70 V/m，电场左边是足够长、宽度L2＝0.2 m、磁感应强度B＝2×10－3 T的有界匀强磁场。一带电粒子电荷量q=＋3.2×10-19C，质量m＝6.4×10－27 kg，以v＝4×104 m/s的速度沿OO′垂直射入磁场，在磁场中偏转后进入右侧的电场，最后从电场右边界射出。（粒子重力不计）求：
（1）带电粒子在磁场中运动的轨道半径和时间；
（2）带电粒子飞出电场时的速度大小。
半径R = 40cm竖直放置的光滑圆轨道与水平直轨道相连接（如图所示）。质量m = 50g的小球A以一定的初速度由直轨道向左运动，并沿圆轨道的内壁冲上去。如果A经过N点时的速度v1= 6m/s，A经过轨道最高点M后作平抛运动，平抛的水平距离为1.6m。求：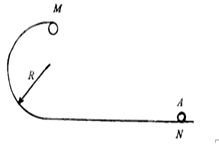
（1）小球经过M时速度多大；
（2）小球经过M时对轨道的压力多大；
（3）小球从N点滑到轨道最高点M的过程中克服摩擦力做的功是多少。（g=10m/s2）
如图所示，一水平传送带始终保持着大小为v0＝4m/s的速度做匀速运动。在传送带右侧有一半圆弧形的竖直放置的光滑圆弧轨道，其半径为R=0.2m，半圆弧形轨道最低点与传送带右端B衔接并相切，一小物块无初速地放到皮带左端A处，经传送带和竖直圆弧轨道至最高点C。已知当A、B之间距离为s=1m时，物块恰好能通过半圆轨道的最高点C，（g=10m/s2）则：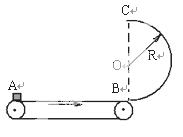
(1) 物块至最高点C的速度v为多少?
(2) 物块与皮带间的动摩擦因数为多少？
(3) 若只改变传送带的长度，使滑块滑至圆弧轨道的最高点C 时对轨道的压力最大，传送带的长度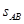
应满足什么条件？
一种氢气燃料的汽车，质量为m = 2.0×103kg ，发动机的额定输出功率为P额="80kW" ，行驶在平直公路上时所受阻力恒为车重的0.1倍。若汽车从静止开始先匀加速启动，加速度的大小为a = 1.0m/s2。达到额定输出功率后，汽车保持功率不变又加速行驶了s="800m" ，直到获得最大速度后才匀速行驶。（g取10m/s2）。试求：
（1）汽车的最大行驶速度；
（2）汽车匀加速阶段结束时的速度；
（3）汽车以额定功率又加速了多长时间？
某战士在倾角θ = 30°的山坡上进行投掷手榴弹训练。他从A点以某一初速度υ0沿水平方向投出手榴弹，正好落在B点，测得AB 间的距离L= 90m。设空气阻力不计，取重力加速度g = 10m/s2。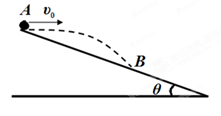
（1）该型号手榴弹从拉动弦到爆炸需要T=5s的时间，若要求手榴弹正好落地爆炸，求战士从拉动弦到投出所用时间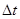
；
（2）求手榴弹抛出的初速度
大小。