四棱锥P—ABCD的底面是边长为2的菱形,∠DAB=60°,侧棱 ,
,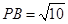 ,M、N两点分别在侧棱PB、PD上,
,M、N两点分别在侧棱PB、PD上,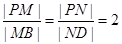 .
.
(1)求证:PA⊥平面MNC。
(2)求平面NPC与平面MNC的夹角的余弦值.
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,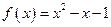 。
。
(1)求函数 的解析式;
的解析式;
(2)求不等式 的解集。
的解集。
设函数 的定义域是R,对于任意实数
的定义域是R,对于任意实数 ,恒有
,恒有 ,且当
,且当 时,
时, .
.
(Ⅰ)求证: ,且当
,且当 时,有
时,有 ;
;
(Ⅱ)判断 在R上的单调性;
在R上的单调性;
(Ⅲ)设集合 ,集合
,集合 ,若
,若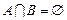 ,求
,求 的取值范围.
的取值范围.
设函数f(x)=x2+(lga+2)x+lgb,g(x)=2x+2,若f(-1)=0,且对一切实数x,不等式f(x)≥g(x)恒成立;
(Ⅰ)(本问5分)求实数a、b的值;
(Ⅱ)(本问7分)设F(x)=f(x)-g(x),数列{an}满足关系an=F(n),
证明: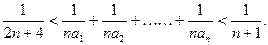
已知 ,
, ,3].
,3].
(1)求f(x);
(2)求 ;
;
(3)在f(x)与 的公共定义域上,解不等式f(x)>
的公共定义域上,解不等式f(x)> +
+ .
.
设a>0,函数f(x)= -ax在[1,+∞)上是单调函数.
-ax在[1,+∞)上是单调函数.
(1)求实数a的取值范围;
(2)设 ≥1,f(x)≥1,且f(f(
≥1,f(x)≥1,且f(f( ))=
))= ,求证:f(
,求证:f( )=
)= .
.