如图,将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE= .
.
(1)若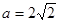 ,求证:AB∥平面CDE;
,求证:AB∥平面CDE;
(2)求实数 的值,使得二面角AECD的大小为60°.
的值,使得二面角AECD的大小为60°.
(本小题满分13分)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在一次游戏中,
(i)摸出3个白球的概率;
(ii)获奖的概率;
(Ⅱ)求在两次游戏中获奖次数 的分布列.
的分布列.
(本小题满分12分)已知函数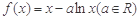
(1)当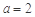 时,求曲线
时,求曲线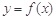 在点
在点 处的切线方程;
处的切线方程;
(2)求函数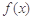 的极值.
的极值.
(本小题满分12分)证明: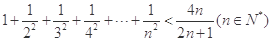 .
.
六人按下列要求站一横排,分别有多少种不同的站法?
(l)甲不站两端;
(2)甲、乙不相邻;
(3)甲、乙之间间隔两人;
(4)甲不站左端,乙不站右端.
若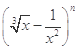 的展开式的二项式系数和为128.
的展开式的二项式系数和为128.
(1)求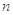 的值;
的值;
(2)求展开式中的常数项;
(3)求展开式中二项式系数的最大项.