规律是数学研究的重要内容之一．初中数学中研究的规律主要有一些特定的规则、符号(数)及其运算规律、图形的数值特征和位置关系特征等方面．
请你解决以下与数的表示和运算相关的问题：
(1)写出奇数a用整数n表示的式子；
(2)写出有理数b用整数m和整数n表示的式子；
(3)函数的研究中，应关注y随x变化而变化的数值规律(课本里研究函数图象的特征实际上也是为了说明函数的数值规律)．
下面对函数y＝x2的某种数值变化规律进行初步研究：
| xi |
0 |
1 |
2 |
3 |
4 |
5 |
… |
| yi |
0 |
1 |
4 |
9 |
16 |
25 |
… |
| yi＋1－yi |
1 |
3 |
5 |
7 |
9 |
11 |
… |
由表看出，当x的取值从0开始每增加1个单位时，y的值依次增加1，3，5…
请回答：
①当x的取值从0开始每增加
个单位时，y的值变化规律是什么？
②当x的取值从0开始每增加
个单位时，y的值变化规律是什么？
如图，直角梯形纸片ABCD中，AD//BC，∠A=90º，∠C=30º．折叠纸片使BC经过点D，点C落在点E处，BF是折痕，且BF=CF=8．
（1）求∠BDF的度数；
（2）求AB的长．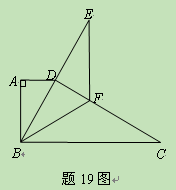
李老师为了解班里学生的作息时间表，调查了班上50名学生上学路上花费的时间，他发现学生所花时间都少于50分钟，然后将调查数据整理，作出如下频数分布直方图的一部分（每组数据含最小值不含最大值）．请根据该频数分布直方图，回答下列问题：
（1）此次调查的总体是什么？
（2）补全频数分布直方图；
（3）该班学生上学路上花费时间在30分钟以上（含30分钟）的人数占全班人数的百分比是多少？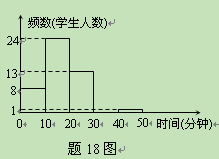
如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路. 现新修一条路AC到公路l. 小明测量出∠ACD=30º，∠ABD=45º，BC=50m. 请你帮小明计算他家到公路l的距离AD的长度（精确到0.1m；参考数据：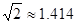
，
）.
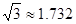某品牌瓶装饮料每箱价格26元．某商店对该瓶装饮料进行“买一送三”促销活
动，若整箱购买，则买一箱送三瓶，这相当于每瓶比原价便宜了0.6元．问该品牌饮料一箱
有多少瓶？
已知抛物线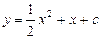
与x轴没有交点．
（1）求c的取值范围；
（2）试确定直线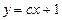
经过的象限，并说明理由．