观察图形,解答问题: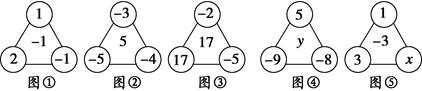
(1)按下表已填写的形式填写表中的空格:
| |
图① |
图② |
图③ |
| 三个角上三个数的积 |
1×(-1)×2=-2 |
(-3)×(-4)×(-5)=-60 |
|
| 三个角上三个数的和 |
1+(-1)+2=2 |
(-3)+(-4)+(-5)=-12 |
|
| 积与和的商 |
-2÷2=-1 |
|
|
(2)请用你发现的规律求出图④中的数y和图⑤中的数x.
如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度 (单位: 与下行时间 (单位: 之间具有函数关系 ,乙离一楼地面的高度 (单位: 与下行时间 (单位: 的函数关系如图2所示.
(1)求 关于 的函数解析式;
(2)请通过计算说明甲、乙两人谁先到达一楼地面.

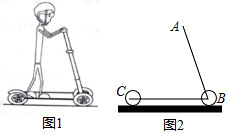
图1是一辆在平地上滑行的滑板车,图2是其示意图.已知车杆 长 ,车杆与脚踏板所成的角 ,前后轮子的半径均为 ,求把手 离地面的高度(结果保留小数点后一位;参考数据: , , .
先化简,再求值: ,其中 .
计算: .
如图,矩形 中, , ,点 , 分别在边 , 上,点 , 分别在边 , 上, , 交于点 ,记 .
(1)若 的值为1,当 时,求 的值.
(2)若 的值为 ,求 的最大值和最小值.
(3)若 的值为3,当点 是矩形的顶点, , 时,求 的值.