已知椭圆C的方程为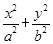 =1(a>b>0),双曲线
=1(a>b>0),双曲线 =1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
=1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
(1)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(2)当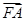 =λ
=λ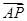 ,求λ的最大值.
,求λ的最大值.
在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.在选取的40名学生中,
( I )求成绩在区间[80,90)内的学生人数;
(Ⅱ)从成绩大于等于80分的学生中随机选2名学生,求至少有1名学生成绩在区间[90,100] 内的概率。
已知 ,且
,且 是第二象限角,求
是第二象限角,求 的值。
的值。
袋子中装有编号为a,b的2个黑球和编号为c,d,e的3个红球,从中任意摸出2个球.
(1)写出所有不同的结果;
(2)求恰好摸出1个黑球和1个红球的概率;
(3) 求至少摸出1个黑球的概率.
在一次射击比赛中,甲、乙两名运动员各射击10次,命中环数如下﹕
甲运动员﹕7,8,6,8,6,5,9,10,7,4;
乙运动员﹕9,5,7,8,7,6,8,6,7,7.
分析上述样本数据,你能判断哪个运动员发挥的更稳定些吗? 如果你是教练,你选择谁去参加比赛?
某射手在一次射击训练中,射中10环、9环、8环、7环的概率分别为0.21,0.23,0.25,0.28,计算该射手在一次射击中:
(1)射中10环或9环的概率;
(2)少于7环的概率。