(18分)如图所示，竖直平面内有无限长、不计电阻的两组平行光滑金属导轨，宽度均为L=0.5m，上方连接一个阻值R=1Ω的定值电阻，虚线下方的区域内存在磁感应强度B=2T的匀强磁场．完全相同的两根金属杆1和2靠在导轨上，金属杆与导轨等宽且与导轨接触良好，电阻均为r=0.5Ω．将金属杆1固定在磁场的上边缘（仍在此磁场内），金属杆2从磁场边界上方h0=0.8m处由静止释放，进入磁场后恰作匀速运动．(g取10m/s2)求：
（1）金属杆的质量m为多大？
（2）若金属杆2从磁场边界上方h1=0.2m处由静止释放，进入磁场经过一段时间后开始匀速运动．在此过程中整个回路产生了1.4J的电热，则此过程中流过电阻R的电量q为多少？
（3）金属杆2仍然从离开磁场边界h1=0.2m处由静止释放，在金属杆2进入磁场的同时由静止释放金属杆1，两金属杆运动了一段时间后均达到稳定状态，试求两根金属杆各自的最大速度．（已知两个电动势分别为E1、E2不同的电源串联时，电路中总的电动势E=E1+E2．）
如下图所示，在竖直平面内固定着半径为R的半圆形轨道，小球B静止在轨道的最低点，小球A从轨道右端正上方3.5R处由静止自由落下，沿圆弧切线进入轨道后，与小球B发生弹性碰撞。碰撞后B球上升的最高点C，圆心O与C的连线与竖直方向的夹角为60°。若两球均可视为质点，不计一切摩擦，求A、B两球的质量之比
.
（1）如图为一列简谐横波在
时的波形图。若波自右向左传播的，则在x=0.2m处且处于平衡位置的P点此时的运动方向是。若经过时间
后，P点刚好第一次到达波峰，则波的传播速度是,从到
时P点走过的路程为。
（2）如图，MN是一条通过透明球体球心的直线。现有一单色细光束AB平行于MN射向球体，B为入射点，若出射光线CD与MN的交点P到球心O的距离是球半径的
倍，且与MN所夹的角
，求此透明体折射率n.
如图所示，在直角坐标xOy平面y轴左侧（含y轴）有一沿y轴负向的匀强电场，一质量为m，电量为q的带正电粒子从x轴上P处以速度
沿x轴正向进入电场，从y轴上Q点离开电场时速度方向与y轴负向夹角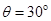
，Q点坐标为（0，-d），在y轴右侧有一与坐标平面垂直的有界匀强磁场区域（图中未画出），磁场磁感应强度大小
，粒子能从坐标原点O沿x轴负向再进入电场．不计粒子重力，求：
（1）电场强度大小E；
（2）如果有界匀强磁场区域为半圆形，求磁场区域的最小面积；
（3）粒子从P点运动到O点的总时间．
2013年9月15日，西安地铁1号线正式通车,西安地铁正式进入换乘时代。已知相距4000 m的甲乙两站之间的线路为直线，在调试运行时，列车出站加速和进站减速的加速度大小均为1 m/s2，中途保持匀速运行。列车从甲站由静止出发到乙站停止正好用时4 min。某次调试时，列车从甲站出发比原定的出发时间晚了20s，但仍保持与原来相同的加速度出站和进站，要使列车仍然准点到达乙站，求此次列车出站加速的时间应为多少？
在竖直平面内固定一半径为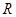
的金属细圆环，质量为
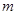的金属小球（视为质点）通过长为
的绝缘细线悬挂在圆环的最高点．当圆环、小球都带有相同的电荷量
（未知）时，发现小球在垂直圆环平面的对称轴上处于平衡状态，如图所示．已知静电力常量为
,则有( ) 
A．绳对小球的拉力 |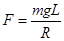
B．电荷量 |
C．绳对小球的拉力 |
D．电荷量 |