设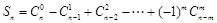 ,
, 且
且 ,其中当
,其中当 为偶数时,
为偶数时, ;当
;当 为奇数时,
为奇数时,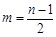 .
.
(1)证明:当 ,
,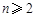 时,
时,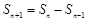 ;
;
(2)记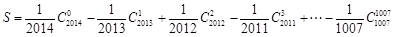 ,求
,求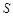 的值.
的值.
(本小题满分12分) 若函数 的图象与直线
的图象与直线 相切,相邻切点之
相切,相邻切点之
间的距离为 。
。
(Ⅰ)求 和
和 的值;
的值;
(Ⅱ)若点 是
是 图象的对称中心,且
图象的对称中心,且 ,求点
,求点 的坐标。
的坐标。
(13分)一个同心圆形花坛,分为两部分,中间小圆部分种植绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.
⑴ 如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?
如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
⑵ 如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?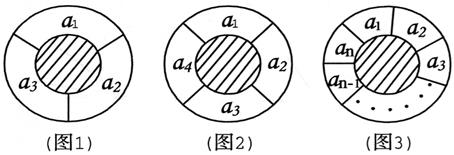
(12分) 已知数列 (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.
(1)求和: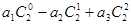 ,
,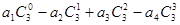
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
(13分) 已知 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求n的值;
(2)求展开式中系数最大的项.
(12分) 由0,1,2,3,4,5这六个数字。
(1)能组成多少个无重复数字的四位数?
(2)能组成多少个无重复数字的四位偶数?
(3)能组成多少个无重复数字且被25个整除的四位数?
(4)组成无重复数字的四位数中比4032大的数有多少个?