如图,已知△OAB的顶点A(-6,0),B(0,2),O是坐标原点, 将△OAB绕点O按顺时针旋转90°,得到△ODC.
(1)写出C点的坐标为 ;
(2)设过A,D,C三点的抛物线的解析式为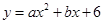 ,求其解析式?
,求其解析式?
(3)证明AB⊥BE.
如图,在直角坐标系中,以点A(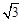 ,0)为圆心,以
,0)为圆心,以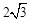 为半径圆与x轴相交于点B,C,与y轴相交于点D,E.
为半径圆与x轴相交于点B,C,与y轴相交于点D,E.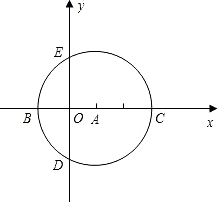
(1)若抛物线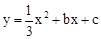 经过点C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
经过点C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
(2)在(1)中的抛物线的对称轴上有一点P,使得△PBD的周长最小,求点P的坐标;
(3)设Q为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点M,使得四边形BCQM是平行四边形?若存在,求出点M的坐标;若不存在,说明理由.
如图,矩形ABCD为一本书,AB=12π,AD=2,当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧),如第一张纸AB对应为 ,最后一张纸CD对应为
,最后一张纸CD对应为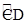 (
(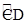 为半圆),
为半圆),
(1)连结OB,求钝角∠AOB=;
(2)如果该书共有100张纸,求第40张纸对应的弧超出半圆部分的长.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点C距守门员多少米?(取 )
)
(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取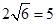 )
)
如图,点A、B、C是⊙O上的三点,AB∥OC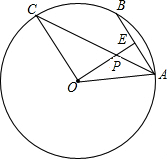
(1)求证:AC平分∠OAB.
(2)过点O作OE⊥AB于点E,交AC于点P.若AB=2,∠AOE=30°,求PE的长.
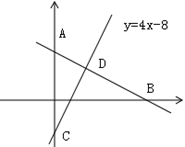
如图,已知直线l与y轴、x轴交于点A(0,8)、B(6,0)两点,直线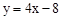 与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积。
与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积。