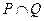(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)若 ,使
,使 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(3)若函数 的图象在区间(1,+∞)内恒在直线
的图象在区间(1,+∞)内恒在直线 下方,求实数
下方,求实数 的取值范围.
的取值范围.
(1)当 时,求椭圆的标准方程及其右准线的方程;
时,求椭圆的标准方程及其右准线的方程;
(2)用 表示P点的坐标;
表示P点的坐标;
(3)是否存在实数 ,使得
,使得 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数 ;若不存在,请说明理由.
;若不存在,请说明理由.
(1)当车速为 (千米/小时)时,从甲地到乙地的耗油量为
(千米/小时)时,从甲地到乙地的耗油量为 (升),求函数
(升),求函数 的解析式并指出函数的定义域;
的解析式并指出函数的定义域;
(2)当车速为多大时,从甲地到乙地的耗油量最少




(1)证明: ;
;
(2)当 点为线段
点为线段 的中点时,求异面直线
的中点时,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)试问E点在何处时,平面 与平面
与平面 所成二面角的平面角的余弦值为
所成二面角的平面角的余弦值为 .
.
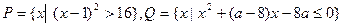
(1) 求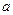 的一个值,使它成为
的一个值,使它成为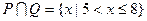 的一个充分不必要条件;
的一个充分不必要条件;
(2) 求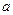 的取值范围,使它成为
的取值范围,使它成为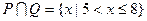 的充要条件;
的充要条件;
(3) 求