如图所示，MPQO为有界的竖直向下的匀强电场（边界上有电场），电场强度为E=mg/q，ACB为光滑固定的半圆形轨道，轨道半径为R，A、B为圆水平直径的两个端点，AC为
圆弧。一个质量为m，电荷量为－q的带电小球，从A点正上方高为H=R处由静止释放，并从A点沿切线进入半圆轨道，不计空气阻力及一切能量损失，关于带电小球的受力及运动情况，下列说法正确的是（ ）
A.小球到达C点时对轨道压力为3 mg
B.小球在AC部分运动时，加速度不变
C.适当增大E，小球到达C点的速度可能为零
D.若E=2mg/q，要使小球沿轨道运动到C，则应将H至少调整为3R/2
已知太阳到地球与地球到月球的距离的比值约为390,月球绕地球旋转的周期约为27天.利用上述数据以及日常的天文知识,可估算出太阳对月球与地球对月球的万有引力的比值约为()
| A．0.2 | B．2 |
| C．20 | D．200 |
某宇宙飞船在月球上空以速度v绕月球做圆周运动.如图,为了使飞船较安全地落在月球上的B点,在轨道A点点燃火箭发动器做出短时间的发动,向外喷射高温燃气,喷气的方向为( )
| A．与v的方向相反 |
| B．与v的方向一致 |
| C．垂直v的方向向右 |
| D．垂直v的方向向左 |
火星直径为地球的一半,质量约为地球的十分之一,它绕太阳公转的轨道半径约为地球公转半径的1.5倍.根据以上数据,以下说法正确的是( )
| A．火星表面重力加速度的数值比地球表面的小 |
| B．火星公转的周期比地球的长 |
| C．火星公转的线速度比地球的大 |
| D．火星公转的向心加速度比地球的大 |
如右图所示,圆a的圆心在地球自转的轴线上,圆b、c、d的圆心均在地球的地心上,对绕地球做匀速圆周运动的人造地球卫星而言,下列说法错误的是( )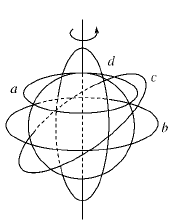
| A．卫星的轨道可能为a |
| B．同步卫星的轨道只能为b |
| C．卫星的轨道可能为c |
| D．卫星的轨道可能为d |
如图是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测.下列说法正确的是( )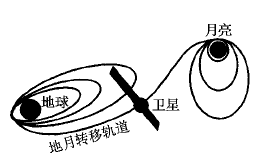
| A．发射“嫦娥一号”的速度必须达到第三宇宙速度 |
| B．在绕月圆轨道上,卫星周期与卫星质量有关 |
| C．卫星受月球的引力与它到月球中心距离的平方成反比 |
| D．在绕月圆轨道上,卫星受地球的引力大于受月球的引力 |