在高中“自选模块”考试中，某考场的每位同学都选了一道数学题，第一小组选《数学史与不等式选讲》的有1人，选《矩阵变换和坐标系与参数方程》的有5人，第二小组选《数学史与不等式选讲》的有2人，选《矩阵变换和坐标系与参数方程》的有4人，现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4人均为选《矩阵变换和坐标系与参数方程》的概率；
(2)设X为选出的4个人中选《数学史与不等式选讲》的人数，求X的分布列和数学期望．
设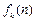
为关于n的k
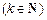次多项式．数列{an}的首项
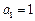，前n项和为
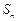．对于任意的正整数n，
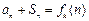都成立．
（1）若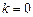
，求证：数列{an}是等比数列；
（2）试确定所有的自然数k，使得数列{an}能成等差数列
若函数
为定义域
上单调函数，且存在区间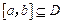
（其中
），使得当
时，的取值范围恰为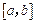
，则称函数是上的正函数，区间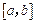叫做等域区间．
（1）已知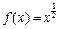
是
上的正函数，求的等域区间；
（2）试探究是否存在实数
，使得函数
是
上的正函数？若存在，请求出实数的取值范围；若不存在，请说明理由
如图，某兴趣小组测得菱形养殖区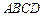
的固定投食点
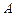到两条平行河岸线
的距离分别为4m、8m，河岸线
与该养殖区的最近点
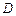的距离为1m，
与该养殖区的最近点
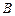的距离为2m．
（1）如图甲，养殖区在投食点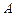的右侧，若该小组测得
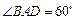，请据此算出养殖区的面积；
（2）如图乙，养殖区在投食点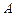的两侧，试在该小组未测得
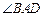的大小的情况下，估算出养殖区的最小面积．
在△ABC中，角A，B，C的对边分别是a，b，c，且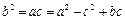
．
（1）求
的值；
（2）试判断△ABC的形状，并说明理由
设定义在
上的函数
的最小正周期为
．
（1）若
，
，求的最大值；
（2）若
，
，求
的值