某地位于甲、乙两条河流的交汇处,根据统计资料预测,今年汛期甲河流发生洪水的概率为0.25,乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响).现有一台大型设备正在该地工作,为了保护设备,施工部门提出以下三种方案:
方案1:运走设备,此时需花费4000元;
方案2:建一保护围墙,需花费1000元,但围墙只能抵御一个河流发生的洪水,当两河流同时发生洪水时,设备仍将受损,损失约56000元;
方案3:不采取措施,此时,当两河流都发生洪水时损失达60000元,只有一条河流发生洪水时,损失为10000元.
(1)试求方案3中损失费X(随机变量)的分布列;
(2)试比较哪一种方案好.
如图,在四棱锥 中,底面
中,底面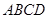 是矩形,
是矩形, 底面
底面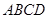 ,
, 是
是 的中点,已知
的中点,已知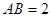 ,
, ,
,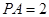 ,求:(Ⅰ)三角形
,求:(Ⅰ)三角形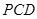 的面积;(II)三棱锥
的面积;(II)三棱锥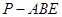 的体积
的体积
为加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,教育部门主办了全国中学生航模竞赛. 该竞赛分为预赛和决赛两个阶段,参加决赛的队伍按照抽签方式决定出场顺序.通过预赛,选拔出甲、乙、丙和丁四支队伍参加决赛.
(Ⅰ)求决赛中甲、乙两支队伍恰好排在前两位的概率;
⑾求决赛中甲、乙两支队伍出场顺序相邻的概率.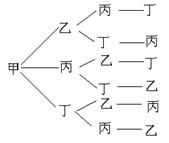
在△ 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知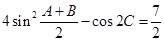 ,且
,且 ,
,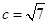 ,求: (Ⅰ)
,求: (Ⅰ) .⑾△
.⑾△ 的面积.
的面积.
设双曲线C: -y2=1的左、右顶点分别为A1、A2,垂直于x轴的直线m与双曲线C交于不同的两点P、Q.
-y2=1的左、右顶点分别为A1、A2,垂直于x轴的直线m与双曲线C交于不同的两点P、Q.
(1)若直线m与x轴正半轴的交点为T,且 ·
·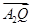 =1,求点T的坐标;
=1,求点T的坐标;
(2)求直线A1P与直线A2Q的交点M的轨迹E的方程;
(3)过点F(1,0)作直线l与(2)中的轨迹E交于不同的两点A、B,设 =λ·
=λ· ,若λ∈[-2,-1],求|
,若λ∈[-2,-1],求| +
+ |(T为(1)中的点)的取值范围.
|(T为(1)中的点)的取值范围.
已知函数f(x)=2x- -aln(x+1),a∈R.
-aln(x+1),a∈R.
(1)若a=-4,求函数f(x)的单调区间;
(2)求y=f(x)的极值点(即函数取到极值时点的横坐标).