数列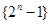 的前
的前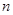 项组成集合
项组成集合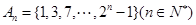 ,从集合
,从集合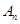 中任取
中任取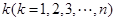 个数,其所有可能的
个数,其所有可能的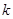 个数的乘积的和为
个数的乘积的和为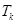 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记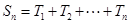 .例如:当
.例如:当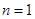 时,
时,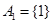 ,
,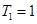 ,
,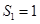 ;当
;当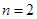 时,
时,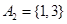 ,
,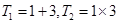 ,
,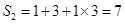 .
.
(Ⅰ)求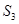 ;
;
(Ⅱ)猜想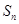 ,并用数学归纳法证明.
,并用数学归纳法证明.
过抛物线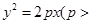

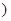 的对称轴上的定点
的对称轴上的定点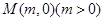 ,作直线
,作直线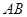 与抛物线相交于
与抛物线相交于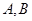 两点.
两点.
(I)试证明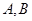 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(II)若点 是定直线
是定直线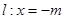 上的任一点,试探索三条直线
上的任一点,试探索三条直线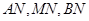 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米,
(I)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(II)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
(Ⅲ)若AN的长度不少于6米,则当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积. 
在四棱锥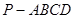 中,
中,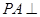 平面
平面 ,底面
,底面 为矩形,
为矩形,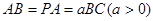 .
.
(Ⅰ)当 时,求证:
时,求证: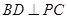 ;
;
(Ⅱ)若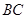 边上有且只有一个点
边上有且只有一个点 ,使得
,使得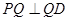 ,求此时二面角
,求此时二面角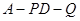 的余弦值.
的余弦值.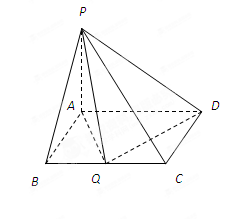
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
 视觉 视觉 |
视觉记忆能力 |
||||
| 偏低 |
中等 |
偏高 |
超常 |
||
| 听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
| 中等 |
1 |
8 |
3 |
 |
|
| 偏高 |
2 |
 |
0 |
1 |
|
| 超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为 .
.
(I)试确定 、
、 的值;
的值;
(II)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(III)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为 ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.
在△ABC中, 为三个内角
为三个内角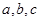 为三条边,
为三条边, 且
且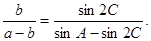
(I)判断△ABC的形状;
(II)若 ,求
,求 的取值范围.
的取值范围.