已知椭圆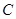 :
: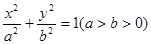 的离心率为
的离心率为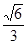 ,右焦点为(
,右焦点为( ,0).
,0).
(1)求椭圆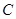 的方程;
的方程;
(2)若过原点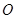 作两条互相垂直的射线,与椭圆交于
作两条互相垂直的射线,与椭圆交于 ,
,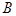 两点,求证:点
两点,求证:点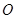 到直线
到直线 的距离为定值.
的距离为定值.
(本小题满分14分)
已知函数
(1)若 ,求
,求 的单调递减区间;
的单调递减区间;
(2)若 ,求
,求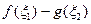 的最小值;
的最小值;
(3)若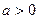 ,且存在
,且存在 使得
使得 ,求实数
,求实数 的取值范围。
的取值范围。
(本小题满分14分)
如图,F1、F2分别是椭圆 的左右焦点,M为椭圆上一点,MF2垂直于
的左右焦点,M为椭圆上一点,MF2垂直于 轴,椭圆下顶点和右顶点分别为A,B,且
轴,椭圆下顶点和右顶点分别为A,B,且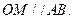
(1)求椭圆的离心率;
(2)过F2作OM垂直的直线交椭圆于点P,Q,若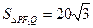 ,求椭圆方程。
,求椭圆方程。
(本 小题满分14分)
小题满分14分)
已知函数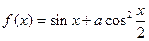 ,其中
,其中 为常数,且
为常数,且 是函数
是函数 的一个零点。
的一个零点。
(1)求函数 的最小正周期;
的最小正周期;
(2)当 时,求函数
时,求函数 的值域。
的值域。
(本小题满分7分)选修4-4;坐标系与参数方程
已知直线 经过点M(1,3),且倾斜角为
经过点M(1,3),且倾斜角为 ,圆C的参数方程为
,圆C的参数方程为 (
( 是参数),直线
是参数),直线 与圆C交于P1、P2两
与圆C交于P1、P2两 点,求P1、P2两点间的距离。
点,求P1、P2两点间的距离。
本题(1)、(2)两个必答题,每小题7分,满分14分。
(1)(本小题满分7分)选修4-2;矩阵与变换
曲线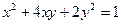 在二阶矩阵
在二阶矩阵 的作用下变换为曲线
的作用下变换为曲线
1)求实数 的值;
的值;
2)求M的逆矩阵M-1。