如图，在长方体ABCD－A1B1C1D1中，底面A1B1C1D1是正方形，O是BD的中点，E是棱AA1上任意一点．
(1)证明：BD⊥EC1；
(2)如果AB＝2，AE＝
，OE⊥EC1，求AA1的长．
已知单调递增的等比数列{an}满足：
a2＋a3＋a4＝28，且a3＋2是a2和a4的等差中项．
(1)求数列{an}的通项公式an；
(2)令bn＝anlog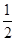
an，Sn＝b1＋b2＋…＋bn，求使Sn＋n·2n＋1>50成立的最小的正整数n.
设数列{an}满足a1＝2，a2＋a4＝8，且对任意n∈N*，函数f(x)＝(an－an＋1＋an＋2)x＋an＋1cos x－an＋2sin x满足f′
＝0.
(1)求数列{an}的通项公式；
(2)若bn＝2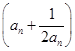
，求数列{bn}的前n项和Sn.
设数列{an}的前n项和为Sn，数列{Sn}的前n项和为Tn，满足Tn＝2Sn－n2，n∈N*.
(1)求a1的值；
(2)求数列{an}的通项公式．
在公差为d的等差数列{an}中，已知
a1＝10，且a1,2a2＋2,5a3成等比数列．
(1)求d，an；
(2)若d<0，求|a1|＋|a2|＋…＋|an|.
小题满分14分）
，其中
为常数，且
是函数
的一个零点。
时，求函数