设数列{an}满足a1＝2，a2＋a4＝8，且对任意n∈N*，函数f(x)＝(an－an＋1＋an＋2)x＋an＋1cos x－an＋2sin x满足f′
＝0.
(1)求数列{an}的通项公式；
(2)若bn＝2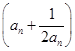
，求数列{bn}的前n项和Sn.
已知抛物线
的方程为
，点
在抛物线上．
（1）求抛物线的方程；
（2）过点
作直线交抛物线于不同于
的两点
，若直线
分别交直线
于
两点，求
最小时直线
的方程．
如图，在矩形
中，
，点
在边
上，点
在边
上，且
，垂足为
，若将
沿
折起，使点
位于
位置，连接
，得四棱锥
．
(1)求证：平面
平面
；
(2)若
，直线
与平面
所成角的大小为
，求直线
与平面
所成角的正弦值．
已知
,其中
（1）当
时，求函数
的最大值和最小值，并写出相应的
的值．
（2）若在R上恒为增函数，求实数
的取值范围．
已知
是关于
的二次方程
的两个实数根，求：（1）
的值；
（2）
的值．
已知命题
：直线
与抛物线
有两个交点；命题
：关于
的方程
有实根．若
为真命题，
为假命题，求实数
的取值范围．