如图是多面体 和它的三视图.
和它的三视图.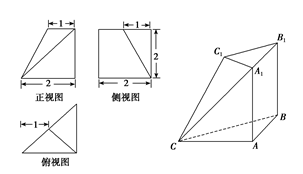
(1)若点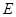 是线段
是线段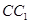 上的一点,且
上的一点,且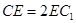 ,求证:
,求证: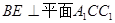 ;
;
(2)求二面角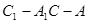 的余弦值.
的余弦值.
设有关于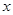 的一元二次方程
的一元二次方程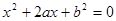
(1)若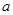 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,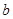 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若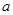 是从区间[0,3]任取的一个数,
是从区间[0,3]任取的一个数,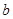 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.
已知数列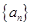 是等差数列,
是等差数列, ,数列
,数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列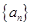 的通项公式;
的通项公式;
(2)记 ,若
,若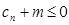 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知关于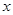 的不等式
的不等式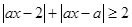
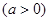 .
.
(1)当 时,求此不等式的解集;(2)若此不等式的解集为R,求实数
时,求此不等式的解集;(2)若此不等式的解集为R,求实数 的取值范围.
的取值范围.
已知圆x2+y2-2ax-6ay+10a2-4a=0(0<a 4)的圆心为C,直线L: y=x+m。
4)的圆心为C,直线L: y=x+m。
(1)若a=2,求直线L被圆C所截得的弦长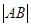 的最大值;
的最大值;
(2)若m=2,求直线L被圆C所截得的弦长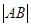 的最大值;
的最大值;