已知关于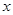 的不等式
的不等式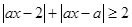
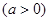 .
.
(1)当 时,求此不等式的解集;(2)若此不等式的解集为R,求实数
时,求此不等式的解集;(2)若此不等式的解集为R,求实数 的取值范围.
的取值范围.
已知函数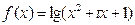
(1)当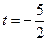 ,求函数
,求函数 的定义域;
的定义域;
(2)当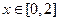 ,求
,求 的最小值(用
的最小值(用 表示);
表示);
(3)是否存在不同的实数 ,使得
,使得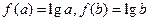 ,并且
,并且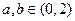 ,若存在,求出实数
,若存在,求出实数 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
已知函数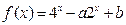 ,当
,当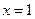 时,
时,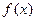 有最小值
有最小值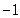 ;
;
(1)求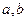 的值;(2)求满足
的值;(2)求满足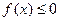 的
的 的集合
的集合 ;
;
统计某校100名学生的数学会考成绩,得到样本频率分布直方图如右图示,规定不低于60分为及格,不低于85分为优秀,
(1)估计这次考试的及格人数和优秀率;
( 2)从成绩是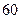 分以下(包括
分以下(包括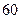 分)的学生中选两人,求他们不在同一分数段的概率.
分)的学生中选两人,求他们不在同一分数段的概率.
 |
已知角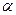 满足
满足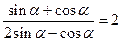 ;
;
(1)求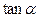 的值;(2)求
的值;(2)求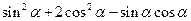 的值
的值
已知三角形ABC的顶点坐标为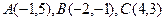 ,M是BC边上的中点.
,M是BC边上的中点.
⑴求AB边所在直线的方程;
⑵求中线AM的长.