已知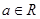 ,命题
,命题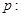 “
“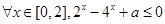 均成立”,命题
均成立”,命题 “函数
“函数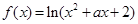 定义域为R”.
定义域为R”.
(1)若命题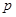 为真命题,求实数
为真命题,求实数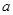 的取值范围;
的取值范围;
(2)若命题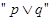 为真命题,命题
为真命题,命题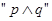 为假命题,求实数
为假命题,求实数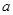 的取值范围.
的取值范围.
(本小题满分13分)
已知圆满足:
①截y轴所得弦长为2;
②被x轴分成两段圆弧,其弧长的比为3:1;
③圆心到直线l:x-2y=0的距离为 ,求该圆的方程.
,求该圆的方程.
(本小题满分13分)
已知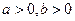 且
且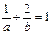 ,求:
,求:
(1)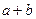 的最小值;
的最小值;
(2)若直线 与
与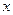 轴、
轴、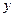 轴分别交于
轴分别交于 、
、 ,求
,求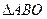 (O为坐标原点)面积的最小值.
(O为坐标原点)面积的最小值.
(本小题满分14分)设函数f(x) =" x2" + bln(x+1),
(1)若对定义域的任意x,都有f(x)≥f(1)成立,求实数b的值;
(2)若函数f(x)在定义域上是单调函数,求实数b的取值范围;
(3)若b = -1,,证明对任意的正整数n,不等式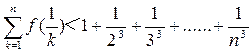 都成立
都成立
(本小题满分13分)椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ,椭圆上的点到焦点的最短距离为1-e, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且 .
.
(1)求椭圆方程;
(2)若 ,求m的取值范围.
,求m的取值范围.
(本小题满分12分)正方体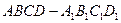 的棱长为
的棱长为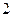 ,
,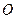 是
是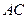 与
与 的交点,
的交点,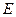 是
是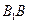 上一点,且
上一点,且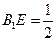 .
.
(1)求证: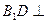 平面
平面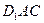 ; (2)求异面直线
; (2)求异面直线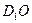 与
与 所成角的余弦值;
所成角的余弦值;
(3)求直线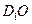 与平面
与平面 所成角的正弦值.
所成角的正弦值.