已知向量m=(sin ωx+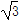 cosωx,1),n=(2cos ωx,-
cosωx,1),n=(2cos ωx,-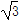 )(ω>0),函数f(x)=m·n的两条相邻对称轴间的距离为
)(ω>0),函数f(x)=m·n的两条相邻对称轴间的距离为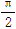 .
.
(1)求函数f(x)的单调递增区间;
(2)当x∈[-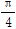 ,
,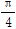 ] 时,求f(x)的值域.
] 时,求f(x)的值域.
设函数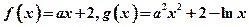 ,其中
,其中 ,
,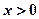 。
。
(1)若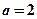 ,求曲线
,求曲线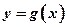 在
在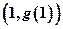 点处的切线方程;
点处的切线方程;
(2)是否存在负数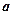 ,使
,使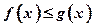 对一切正数
对一切正数 都成立?若存在,求出
都成立?若存在,求出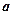 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
已知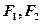 分别是椭圆
分别是椭圆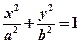
 的左、右 焦点,已知点
的左、右 焦点,已知点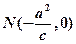 满足
满足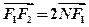 ,且
,且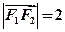 。设
。设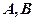 是上半椭圆上且满足
是上半椭圆上且满足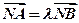 的两点。
的两点。
(1)求此椭圆的方程;
(2)若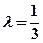 ,求直线AB的斜率。
,求直线AB的斜率。
已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元。设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为R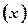 万元,且R
万元,且R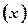
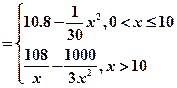
(1)写出年利润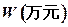 关于年产量
关于年产量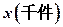 的函数解析式;
的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。
(注:年利润=年销售收入-年总成本)
如图: PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD= ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(Ⅰ)求三棱锥E-PAD的体积;
(Ⅱ)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅲ)证明:无论点E在边BC的何处,都有PE⊥AF.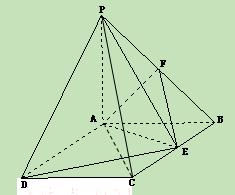
已知函数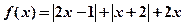 ,
,
(Ⅰ)求函数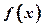 的最小值;(Ⅱ)已知
的最小值;(Ⅱ)已知 ,命题p:关于x的不等式
,命题p:关于x的不等式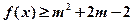 对任意
对任意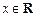 恒成立;命题
恒成立;命题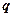 :指数函数
:指数函数 是增函数.若“p或q”为真,“p且q”为假,求实数
是增函数.若“p或q”为真,“p且q”为假,求实数 的取值范围.
的取值范围.