选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),直线l与曲线
(t为参数),直线l与曲线 交于A,B两点.
交于A,B两点.
(1)求 的长;
的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为 ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
(本小题满分12分)已知函数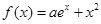 ,
,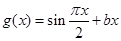 ,直线
,直线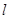 与曲线
与曲线 切于点
切于点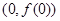 且与曲线
且与曲线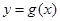 切于点
切于点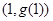 .
.
(1)求a,b的值和直线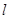 的方程;
的方程;
(2)证明: .
.
(本小题满分12分)已知抛物线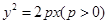 ,过点
,过点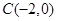 的直线
的直线 交抛物线于A,B两点,坐标原点为O,
交抛物线于A,B两点,坐标原点为O,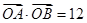 .
.
(1)求抛物线的方程;
(2)当以AB为直径的圆与y轴相切时,求直线 的方程.
的方程.
(本小题满分12分)某城市有东西南北四个进入城区主干道的入口,在早高峰时间段,时常发生交通拥堵现象,交警部门统计11月份30天内的拥堵天数,东西南北四个主干道入口的拥堵天数分别是18天,15天,9天,15天.假设每个入口发生拥堵现象互相独立,视频率为概率.
(1)求该城市一天中早高峰时间段恰有三个入口发生拥堵的概率;
(2)设 表示一天中早高峰时间段发生拥堵的主干道入口个数,求
表示一天中早高峰时间段发生拥堵的主干道入口个数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)如图,四棱锥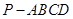 的底面ABCD是平行四边形,
的底面ABCD是平行四边形,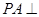 底面ABCD,
底面ABCD,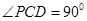 ,
,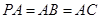 .
.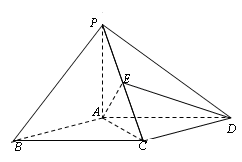
(1)求证: ;
;
(2)点E在棱PC上,满足 ,求二面角
,求二面角 的余弦值.
的余弦值.
(本小题满分12分)在 中,角A,B,C所对的边分别为a,b,c,且
中,角A,B,C所对的边分别为a,b,c,且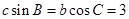 .
.
(1)求b;
(2)若 的面积为
的面积为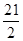 ,求c.
,求c.