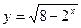如图所示,F1、F2分别为椭圆C: 的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为
的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为 ,
, 的面积为
的面积为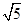 .
.
(1)求椭圆C的方程和焦点坐标;
(2)作与AB平行的直线 交椭圆于P、Q两点,
交椭圆于P、Q两点,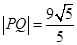 ,求直线
,求直线 的方程.
的方程.
(满分12分) 某商店按每件80元的价格,购进商品1000件(卖不出去的商品将成为废品);市场调研推知:当每件售价为100元时,恰好全部售完;当售价每提高1元时,销售量就减少5件;为获得最大利润,商店决定提高售价 元,获得总利润
元,获得总利润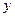 元.
元.
(1)请将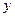 表示为
表示为 的函数;
的函数;
(2)当售价为多少时,总利润取最大值,并求出此时的利润.
函数 是R上的偶函数,且当
是R上的偶函数,且当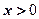 时,函数的解析式为
时,函数的解析式为
(1)求 的值;
的值;
(2)用定义证明 在
在 上是减函数;
上是减函数;
(3)求当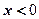 时,函数的解析式;
时,函数的解析式;
已知二次函数的图象如图所示.
(1)写出该函数的零点;
(2)写出该函数的解析式.
(3)求当x∈ 时,函数的值域.
时,函数的值域.
已知集合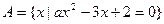 ,问
,问
(1)若集合A中至多有一个元素,求 的取值范围;
的取值范围;
(2)若集合A中至少有一个元素,求 的取值范围。
的取值范围。
求下列函数的定义域:
(1) (2)
(2)