如图,正三棱柱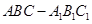 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是 棱的中点,AE交
棱的中点,AE交 于点H.
于点H.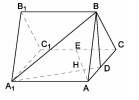
(1)求证: 平面
平面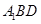 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)求点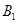 到平面
到平面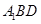 的距离.
的距离.
(本小题满分14分)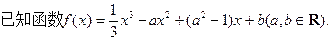
(Ⅰ)若x=1为f(x)的极值点,求a的值;
(Ⅱ)若y= f(x)的图象在点(1,f(1))处的切线方程为x+y-3=0,求f(x)在区间[-2 ,4]上的最大值;
,4]上的最大值;
(Ⅲ )当a≠0时,若f(x)在区间(-1,1)上不单调,求a的取值范围.
)当a≠0时,若f(x)在区间(-1,1)上不单调,求a的取值范围.
(本小题 满分12
满分12 分)
分)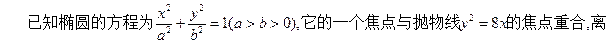
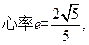 过椭圆的右焦点F作与坐标轴不垂直的直线l交椭圆于A、B两点.
过椭圆的右焦点F作与坐标轴不垂直的直线l交椭圆于A、B两点.
(1)求椭圆的标准方程;
(2)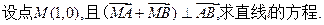
(本小题满分12分)
已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,a2+5>a4,数列{bn}满足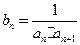 ,其前n项和为Sn.
,其前n项和为Sn.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
(本 小题满分12分)
小题满分12分)
青海玉树发生地震后,为重建,对某项工程进行竞标,现共有6家企业参与竞标,其中A企业来自辽宁省,B、C两家企业来自山东省,D、E、 F三家企业来自河南省,此项工程需要两家企业联合施工,假设每家企业中标的概率相同.
F三家企业来自河南省,此项工程需要两家企业联合施工,假设每家企业中标的概率相同.
(Ⅰ)列举所有企业的中标情况;
(Ⅱ)在中标的企业中,至 少有一家来自山东省的概率是多少?
少有一家来自山东省的概率是多少?
(本小题满分12分)
设函数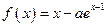 。
。
(I)求函数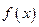 单调区间;
单调区间;
(II)若 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(III)对任意n的个正整数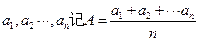
(1)求证: (2)求证:
(2)求证: