已知椭圆C: +
+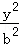 =1(a>b>0)的两个焦点分别为F1(﹣2,0),F2(2,0),离心率为
=1(a>b>0)的两个焦点分别为F1(﹣2,0),F2(2,0),离心率为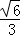 .过焦点F2的直线l(斜率不为0)与椭圆C交于A,B两点,线段AB的中点为D,O为坐标原点,直线OD交椭圆于M,N两点.
.过焦点F2的直线l(斜率不为0)与椭圆C交于A,B两点,线段AB的中点为D,O为坐标原点,直线OD交椭圆于M,N两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)当四边形MF1NF2为矩形时,求直线l的方程.
如图,直三棱柱ABC﹣A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.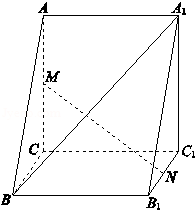
(Ⅰ)求证:MN∥平面ABB1A1;
(Ⅱ)线段CC1上是否存在点Q,使A1B⊥平面MNQ?说明理由.
国家环境标准制定的空气质量指数与空气质量等级对应关系如下表: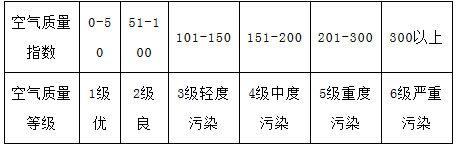
由全国重点城市环境监测网获得2月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图: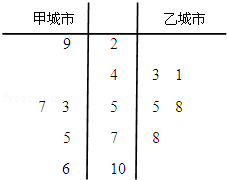
(Ⅰ)试根据上面的统计数据,判断甲、乙两个城市的空气质量指数的方差的大小关系(只需写出结果);
(Ⅱ)试根据上面的统计数据,估计甲城市某一天空气质量等级为2级良的概率;
(Ⅲ)分别从甲城市和乙城市的统计数据中任取一个,试求这两个城市空气质量等级相同的概率.
(注:s2= [(x1﹣
[(x1﹣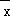 )2+(x2﹣
)2+(x2﹣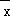 )2+…+(xn﹣
)2+…+(xn﹣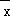 )2],其中
)2],其中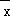 为数据x1,x2,…,xn的平均数.)
为数据x1,x2,…,xn的平均数.)
设{an}是公比为q的等比数列.
(Ⅰ)推导{an}的前n项和Sn公式;
(Ⅱ)设q≠1,证明数列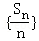 不是等比数列.
不是等比数列.
在△ABC中,已知2sinBcosA=sin(A+C).
(Ⅰ)求角A;
(Ⅱ)若BC=2,△ABC的面积是 ,求AB.
,求AB.