经销商用一辆 型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算,
型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算, 型卡车满载行驶时,每100km所消耗的燃油量
型卡车满载行驶时,每100km所消耗的燃油量 (单位:
(单位: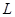 )与速度
)与速度 (单位:km/h)的关系近似地满足
(单位:km/h)的关系近似地满足 ,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
(1)设运送这车水果的费用为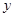 (元)(不计返程费用),将
(元)(不计返程费用),将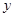 表示成速度
表示成速度 的函数关系式;
的函数关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
如图,平面直角坐标系中,射线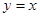 (
(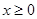 )和
)和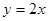 (
(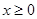 )上分别依次有点
)上分别依次有点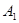 、
、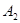 ,……,
,……,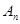 ,……,和点
,……,和点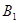 ,
,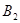 ,……,
,……,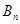 ……,其中
……,其中 ,
,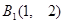 ,
,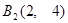 .且
.且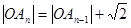 ,
, 
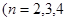 ……).
……).
(1)用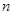 表示
表示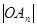 及点
及点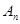 的坐标;
的坐标;
(2)用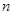 表示
表示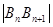 及点
及点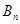 的坐标;
的坐标;
(3)写出四边形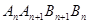 的面积关于
的面积关于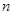 的表达式
的表达式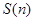 ,并求
,并求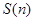 的最大值.
的最大值.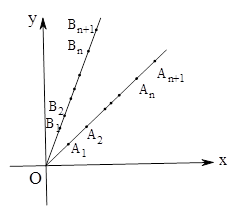
已知:函数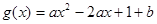
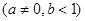 ,在区间
,在区间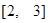 上有最大值4,最小值1,设函数
上有最大值4,最小值1,设函数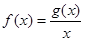 .
.
(1)求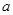 、
、 的值及函数
的值及函数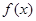 的解析式;
的解析式;
(2)若不等式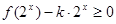 在
在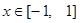 时恒成立,求实数
时恒成立,求实数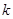 的取值范围;
的取值范围;
(3)如果关于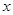 的方程
的方程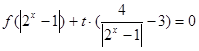 有三个相异的实数根,求实数
有三个相异的实数根,求实数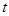 的取值范围.
的取值范围.
已知:曲线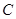 上任意一点到点
上任意一点到点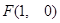 的距离与到直线
的距离与到直线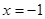 的距离相等.
的距离相等.
(1)求曲线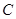 的方程;
的方程;
(2)如果直线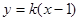 交曲线
交曲线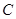 于
于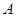 、
、 两点,是否存在实数
两点,是否存在实数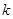 ,使得以
,使得以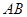 为直径的圆经过原点
为直径的圆经过原点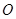 ?若存在,求出
?若存在,求出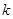 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知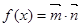 ,其中
,其中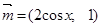 ,
,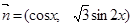
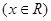 .
.
(1)求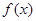 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)在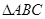 中,
中,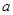 、
、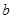 、
、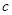 分别是角
分别是角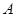 、
、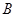 、
、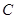 的对边,若
的对边,若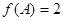 ,
,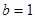 ,
,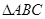 面积为
面积为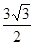 ,求:边
,求:边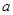 的长及
的长及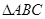 的外接圆半径
的外接圆半径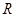 .
.
在长方体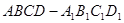 中,
中,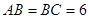 ,用过
,用过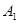 ,
,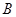 ,
,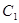 三点的平面截去长方体的一个角后,留下如图的几何体,且这几何体的体积为120.
三点的平面截去长方体的一个角后,留下如图的几何体,且这几何体的体积为120.
(1)求棱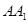 的长;
的长;
(2)求点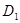 到平面
到平面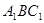 的距离.
的距离.