解分式方程: .
.
(1)计算: ;
;
(2)解不等式 ,并将其解集表示在数轴上.
,并将其解集表示在数轴上.
(本题12分)如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,∠AOC的平分线交AB于点D,E为BC的中点,已知A(0,4)、C(5,0),二次函数 的图象经过A、C两点.
的图象经过A、C两点.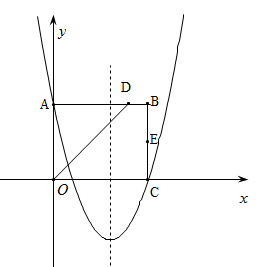

(1)求该二次函数的表达式;
(2)F、G分别为x轴、y轴上的动点,守卫顺次连结D、E、F、G构成四边形DEFG,求四边形DEFG周长的最小值;
(3)抛物线上是否存在点P,使△ODP的面积为12?若存在,求出点P的坐标;若不存在,请说明理由.
在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为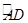 上一点,且
上一点,且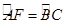 连接DF,并延长DF交BA的延长线于点E.
连接DF,并延长DF交BA的延长线于点E.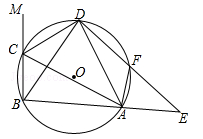
(1)判断DB与DA的数量关系,并说明理由;
(2)求证:△BCD≌△AFD;
(3)若∠ACM=120°,⊙O的半径为5,DC=6,求DE的长.
阅读与应用:阅读1:a、b为实数,且a>0,b>0,因为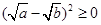 ,所以
,所以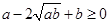 从而
从而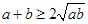 (当a=b时取等号).
(当a=b时取等号).
阅读2:若函数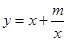 ;(m>0,x>0,m为常数),由阅读1结论可知:
;(m>0,x>0,m为常数),由阅读1结论可知: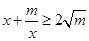 ,所以当
,所以当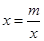 ,即
,即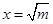 时,函数
时,函数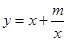 的最小值为
的最小值为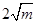 .
.
阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为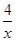 ,周长为2(
,周长为2(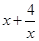 ),求当x=时,周长的最小值为;
),求当x=时,周长的最小值为;
问题2:已知函数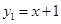 (
(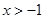 )与函数
)与函数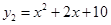 (
(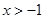 ),
),
当x=时,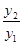 的最小值为;
的最小值为;
问题3:某民办学校每天的支出总费用包含以下三个部分:一是教职工工资4900元;二是学生生活费成本每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)