如图,设 ,且
,且 .当
.当 时,定义平面坐标系
时,定义平面坐标系 为
为 -仿射坐标系,在
-仿射坐标系,在 -仿射坐标系中,任意一点
-仿射坐标系中,任意一点 的斜坐标这样定义:
的斜坐标这样定义: 分别为与
分别为与 轴、
轴、 轴正向相同的单位向量,若
轴正向相同的单位向量,若 ,则记为
,则记为 ,那么在以下的结论中,正确的有.(填上所有正确结论的序号)
,那么在以下的结论中,正确的有.(填上所有正确结论的序号)
①设 、
、 ,若
,若 ,则
,则 ;
;
②设 ,则
,则 ;
;
③设 、
、 ,若
,若 ,则
,则 ;
;
④设 、
、 ,若
,若 ,则
,则 ;
;
⑤设 、
、 ,若
,若 与
与 的夹角
的夹角 ,则
,则 .
.
甲、乙、丙三人在同一办公室工作,办公室只有一部电话机,给该机打进的电话是打给甲、乙、丙的概率分别是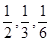 ,在一段时间内该电话机共打进三个电话,且各个电话之间相互独立,则这三个电话中恰有两个是打给乙的概率是(用分数作答)
,在一段时间内该电话机共打进三个电话,且各个电话之间相互独立,则这三个电话中恰有两个是打给乙的概率是(用分数作答)
 =
=
点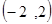 的极坐标为
的极坐标为
正四面体(即四条棱均相等的三棱锥)的4个面上分别写有数字1,2,3,4,将3个这样大小相同、质地均匀的正四面体同时投掷于桌面上。记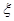 为与桌面接触的3个面上的3个数字中最大值与最小值之差的绝对值,则随机变量
为与桌面接触的3个面上的3个数字中最大值与最小值之差的绝对值,则随机变量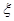 的期望
的期望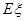 等于。
等于。
对于三次函数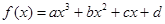 ,定义
,定义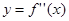 是函数
是函数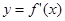 的导函数。若方程
的导函数。若方程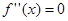 有实数解
有实数解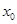 ,则称点
,则称点 为函数
为函数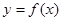 的“拐点”。有同学发现:任何一个三次函数既有拐点,又有对称中心,且拐点就是对称中心。根据这一发现,对于函数
的“拐点”。有同学发现:任何一个三次函数既有拐点,又有对称中心,且拐点就是对称中心。根据这一发现,对于函数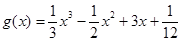 ,
,
则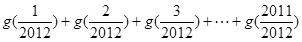 的值为。
的值为。