已知椭圆 (
(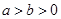 )的短轴长为2,离心率为
)的短轴长为2,离心率为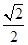 .过点M(2,0)的直线
.过点M(2,0)的直线 与椭圆
与椭圆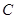 相交于
相交于 、
、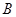 两点,
两点, 为坐标原点.
为坐标原点.
(1)求椭圆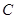 的方程;
的方程;
(2)求 的取值范围;
的取值范围;
(3)若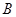 点关于
点关于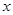 轴的对称点是
轴的对称点是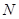 ,证明:直线
,证明:直线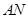 恒过一定点.
恒过一定点.
(本小题满分12分)
如图,在直角坐标系 中,已知椭圆
中,已知椭圆 :
:
 的离心率
的离心率 ,左、右两个焦点分别为
,左、右两个焦点分别为 、
、 。过右焦点
。过右焦点 且与
且与 轴垂直的直线与椭圆
轴垂直的直线与椭圆 相交
相交 、
、 两点,且
两点,且 .
.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左顶点为
的左顶点为 ,下顶点为
,下顶点为 ,动点
,动点 满足
满足 ,试求点
,试求点 的轨迹方程,使点
的轨迹方程,使点 关于该轨迹的对称点落在椭圆
关于该轨迹的对称点落在椭圆 上.
上.
(本小题满分12分)
已知等差数列{an}的首项 ,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
(1)若a1=2,设 ,求数列{cn}的前n项的和Tn;
,求数列{cn}的前n项的和Tn;
(2)在(1)的条件下,若有 的最大值.
的最大值.
(本小题满分12分)
如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.
(I)求证:A1D⊥平面BDE;
(II)求二面角B―DE―C的大小;
(本小题满分12分)
已知函数 .
.
(1)求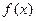 的值域和最小正周期;
的值域和最小正周期;
(2)设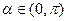 ,且
,且 ,求
,求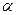 的值.
的值.
.
(本小题满分10分)
在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球5个,白球3个,蓝球2个.现从中任取出一球确定颜色后放回盒子里,再取下一个球.重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球. 求:
(1)最多取两次就结束的概率;
(2)整个过程中恰好取到2个白球的概率;