已知函数 ,其中m,a均为实数.
,其中m,a均为实数.
(1)求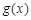 的极值;
的极值;
(2)设 ,若对任意的
,若对任意的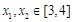
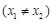 ,
,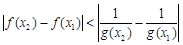 恒成立,求
恒成立,求 的最小值;
的最小值;
(3)设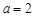 ,若对任意给定的
,若对任意给定的 ,在区间
,在区间 上总存在
上总存在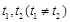 ,使得
,使得 成立,求
成立,求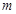 的取值范围.
的取值范围.
如图,平面ABEF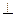 平面ABCD,四边形ABEF与ABCD都是直角梯形,
平面ABCD,四边形ABEF与ABCD都是直角梯形,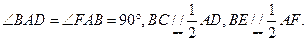
(I)证明:C,D,F,E四点共面;
(II)设AB=BC=BE,求二面角A—ED—B的大小。
(本小题满分12分)
已知 的三
的三 内角A,B,C所对三边分别为a,b,c,且
内角A,B,C所对三边分别为a,b,c,且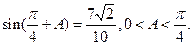
(I)求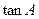 的值。
的值。
(II)若 的面积
的面积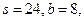 求a的值。
求a的值。
(本小题满分12分)一射击测试每人射击三次,每击中目标一次记10分。没有击中记0分,某人每次击中目标的概率为
(I)求此人得20分的概率;(I I)求此人得分的数学期望与方差。
I)求此人得分的数学期望与方差。
(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个白球,乙盒内有大小相同的2个红球和4个白球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为白球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望.
的分布列和数学期望.
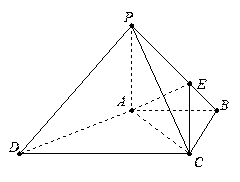
(本小题满分12分)
如图,四棱锥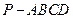 中,
中,
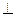 底面
底面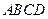 ,
, 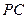
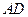 .底面
.底面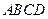 为梯形,
为梯形,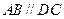 ,
,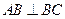 .
. ,点
,点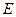 在棱
在棱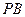 上,且
上,且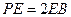 .
.
(1)求证: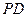
 平面
平面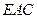 ;
;
(2)求二面角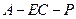 的大小.
的大小.