为了净化空气，某科研单位根据实验得出，在一定范围内，每喷洒1个单位的净化剂，空气中释放的浓度y（单位：毫克/立方米）随着时间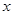
(单位：天)变化的函数关系式近似为
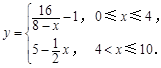若多次喷洒，则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和．由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时，它才能起到净化空气的作用．
（1）若一次喷洒4个单位的净化剂，则净化时间可达几天?
（2）若第一次喷洒2个单位的净化剂，6天后再喷洒a（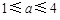
）个单位的药剂，要使接下来的4天中能够持续有效净化，试求
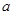的最小值（精确到0.1，参考数据：
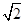取1.4）．
已知四棱锥PABCD的底面ABCD是边长为2的正方形，PD⊥底面ABCD，E，F分别为棱BC，AD的中点．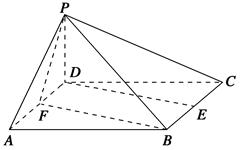
(1)求证：DE∥平面PFB；
(2)已知二面角PBFC的余弦值为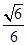
，求四棱锥PABCD的体积．
如图，四边形ABCD是边长为2的正方形，直线l与平面ABCD平行，E和F是l上的两个不同点，且EA＝ED，FB＝FC.E′和F′是平面ABCD内的两点，EE′和FF′都与平面ABCD垂直．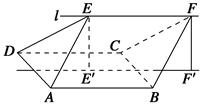
(1)证明：直线E′F′垂直且平分线段AD；
(2)若∠EAD＝∠EAB＝60 °，EF＝2.求多面体ABCDEF的体积．
已知某几何体的俯视图是如图所示的矩形，正视图是一个底边长为8、高为4的等腰三角形，侧视图是一个底边长为6、高为4的等腰三角形．
(1)求该几何体的体积V；
(2)求该几何体的侧面积S.
已知首项为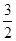
的等比数列{an}不是递减数列，其前n项和为Sn(n∈N*)，且S3＋a3，S5＋a5，S4＋a4成等差数列．
(1)求数列{an}的通项公式；
(2)设Tn＝Sn－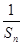
(n∈N*)，求数列{Tn}的最大项的值与最小项的值．
已知函数f(x)＝(x－1)2，g(x)＝4(x－1)，数列{an}是各项均不为0的等差数列，其前n项和为Sn，点(an＋1，S2n－1)在函数f(x)的图象上；数列{bn}满足b1＝2，bn≠1，且(bn－bn＋1)·g(bn)＝f(bn)(n∈N＋)．
(1)求an并证明数列{bn－1}是等比数列；
(2)若数列{cn}满足cn＝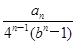
，证明：c1＋c2＋c3＋…＋cn<3.