已知函数f(x)=(x-1)2,g(x)=4(x-1),数列{an}是各项均不为0的等差数列,其前n项和为Sn,点(an+1,S2n-1)在函数f(x)的图象上;数列{bn}满足b1=2,bn≠1,且(bn-bn+1)·g(bn)=f(bn)(n∈N+).
(1)求an并证明数列{bn-1}是等比数列;
(2)若数列{cn}满足cn=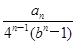 ,证明:c1+c2+c3+…+cn<3.
,证明:c1+c2+c3+…+cn<3.
已知四棱锥 ,底面
,底面 为矩形,侧棱
为矩形,侧棱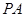 垂直平面
垂直平面 ,
,
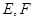 分别为棱
分别为棱 的中点.
的中点.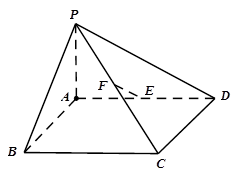
(Ⅰ)证明:
(Ⅱ) 证明: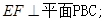
(Ⅲ)求三棱锥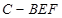 的体积.
的体积.
已知向量 ,
, .
.
(Ⅰ)当 时,求
时,求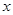 的值;
的值;
(Ⅱ)若向量 与
与 的夹角是锐角,,求
的夹角是锐角,,求 的取值范围.
的取值范围.
韶关某中学高一(19)班的排球队和篮球队各有10名同学,现测得排球队10人的的身高(单位: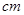 )分别是:
)分别是: 、
、 、
、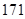 、
、 、
、 、
、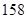 、
、 、
、 、
、 、
、 ,篮球队10人的身高(单位:
,篮球队10人的身高(单位: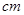 )分别是:
)分别是: 、
、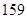 、
、 、
、 、
、 、
、 、
、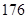 、
、 、
、 、
、 .
.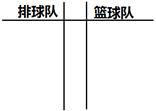
(Ⅰ)请把两队身高数据记录在如图所示的茎叶图中,并指出哪个队的身高数据方差较小(无需计算,只需简单说明理由);
(Ⅱ)现从两队所有身高超过
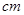 的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率为多小?
的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率为多小?
已知函数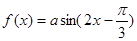 ,且
,且 .
.
(1)求函数 的最大值以及取得最大值时
的最大值以及取得最大值时 的集合;
的集合;
(2)求函数 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
已知函数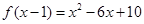 .
.
(1)求函数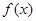 的解析式;
的解析式;
(2)函数 当定义域为
当定义域为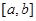 时,值域也为
时,值域也为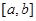 ,则称区间
,则称区间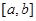 为函数
为函数 的“保值区间”,问:函数
的“保值区间”,问:函数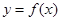 是否存在“保值区间”,若存在求出所有的“保值区间”,若不存在,说明理由.
是否存在“保值区间”,若存在求出所有的“保值区间”,若不存在,说明理由.