本小题满分12分)如图,在四棱锥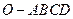 中,底面
中,底面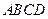 四边长为1的菱形,
四边长为1的菱形, ,
,  ,
, 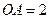 ,
, 为
为 的中点,
的中点,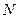 为
为 的中点
的中点
(Ⅰ)证明:直线
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
已知数列a,b,c为各项都是正数的等差数列,公差为d(d>0),在a,b之间和b,c之间共插入m个实数后,所得到的m+3个数所组成的数列{an}是等比数列,其公比为q.
(1)若a=1,m=1,求公差d ;
;
(2)若在a,b之间和b,c之间所插入数的个数均为奇数,求所插入的m数的乘积(用a,c,m表示)
(3)求证:q是无理数.
已知f (x)=ax-ln(-x),x∈(-e,0),g(x)=-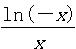 ,其中e是自然常数,a∈R.
,其中e是自然常数,a∈R.
(1)讨论a=-1时, f ( x)的单调性、极值;
x)的单调性、极值;
(2)求证:在(1)的条件下,|f (x)|>g(x)+1/2;
(3)是否存在实数a,使f (x)的最小值是3,如果存在,求出a的值;如果不存在,说明理由.
已知椭圆C: +y2=1,过点(m,0)作圆x2+y2=1的切线l交椭圆G于A、B两点.
+y2=1,过点(m,0)作圆x2+y2=1的切线l交椭圆G于A、B两点.
(1)求椭圆C的焦点坐标和离心率;
(2)将|AB|表示为m的函数,并求|AB|的最大值
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四 个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱
个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱 形状的包装盒,E、
形状的包装盒,E、 F在AB上是被切去的等腰直角
F在AB上是被切去的等腰直角 三角形斜边的两个端点,设AE=FB=xcm.
三角形斜边的两个端点,设AE=FB=xcm.
(1)若广告商要求包装盒侧面积S(cm )最大,试问x
)最大,试问x 应取何值?
应取何值?
(2)若广告商要求包装盒容积V(cm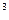 )最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.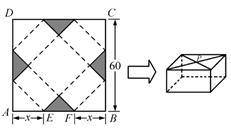
如图,现在要在一块半径为1m.圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设∠BOP=θ,YMNPQ的面积为S.
(1)求S关于θ的函数关系式;
(2)求S的最大值及相应θ的值
1.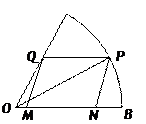
2.