(本小题满分14分)已知函数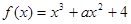 (
(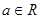 是常数),曲线
是常数),曲线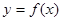 在点
在点 处的切线在
处的切线在 轴上的截距为
轴上的截距为 .
.
(1)求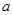 的值;
的值;
(2)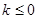 ,讨论直线
,讨论直线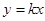 与曲线
与曲线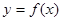 的公共点的个数.
的公共点的个数.
(本小题满分14分)设A是圆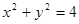 上的任意一点,
上的任意一点,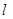 是过点A与
是过点A与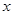 轴垂直的直线,D是直线
轴垂直的直线,D是直线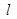 与
与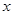 轴的交点,点M在直线
轴的交点,点M在直线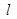 上,且满足
上,且满足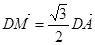 .当点A在圆上运动时,记点M的轨迹为曲线
.当点A在圆上运动时,记点M的轨迹为曲线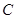 .
.
(1)求曲线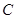 的标准方程;
的标准方程;
(2)设曲线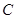 的左右焦点分别为
的左右焦点分别为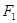 、
、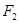 ,经过
,经过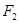 的直线
的直线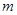 与曲线
与曲线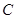 交于P、Q两点,若
交于P、Q两点,若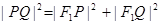 ,求直线
,求直线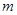 的方程.
的方程.
(本小题满分13分)已知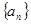 是公差为
是公差为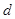 的等差数列,
的等差数列,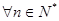 ,
,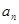 与
与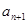 的等差中项为
的等差中项为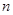 .
.
(1)求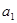 与
与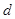 的值;
的值;
(2)设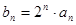 ,求数列
,求数列 的前
的前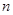 项和
项和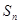 .
.
(本小题满分14分)如图,直角梯形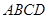 ,
,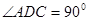 ,
,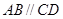 ,
,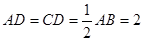 ,点
,点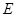 为
为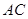 的中点,将
的中点,将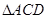 沿
沿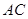 折起,使折起后的平面
折起,使折起后的平面 与平面
与平面 垂直(如图).在下图所示的几何体
垂直(如图).在下图所示的几何体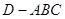 中:
中: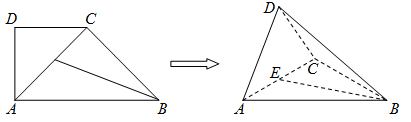
(1)求证: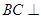 平面
平面 ;
;
(2)点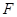 在棱
在棱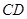 上,且满足
上,且满足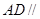 平面
平面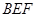 ,求几何体
,求几何体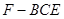 的体积.
的体积.
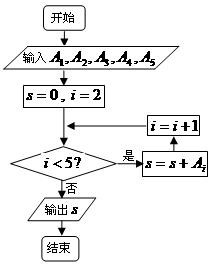
(本小题满分13分)从某企业生产的某种产品中抽取20件,测量这些产品的一项质量指标值,由测量得到如图的频率分布直方图,从左到右各组的频数依次记为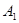 ,
,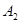 ,
,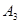 ,
,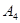 ,
,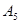 .
.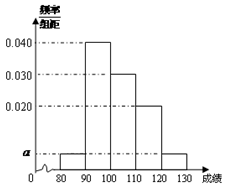
(1)求图中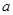 的值;
的值;
(2)下图是统计图中各组频数的一个算法流程图,求输出的结果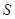 ;
;
(3)从质量指标值分布在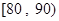 、
、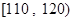 的产品中随机抽取2件产品,求所抽取两件产品的质量指标值之差大于10的概率.
的产品中随机抽取2件产品,求所抽取两件产品的质量指标值之差大于10的概率.