随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康,得到 列联表如下:
列联表如下:
| |
室外工作 |
室内工作 |
合计 |
| 有呼吸系统疾病 |
150 |
|
|
| 无呼吸系统疾病 |
|
100 |
|
| 合计 |
200 |
|
|
(1)补全 列联表;
列联表;
(2)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
(3)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
参考公式与临界值表:K2=
| P(K2≥k0) |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
| k0 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
已知圆 的圆心为
的圆心为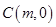 ,
,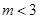 ,半径为
,半径为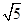 ,圆
,圆 与离心率
与离心率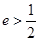 的椭圆
的椭圆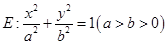 的其中一个公共点为
的其中一个公共点为 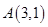 ,
,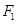 ,
,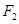 分别是椭圆的左、右焦点.
分别是椭圆的左、右焦点.
(1)求圆 的标准方程;
的标准方程;
(2)若点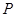 的坐标为
的坐标为 ,试探究直线
,试探究直线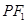 与圆
与圆 能否相切,若能,求出椭圆
能否相切,若能,求出椭圆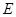 和直线
和直线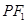 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
如图,三棱柱 中,侧棱
中,侧棱 平面
平面 ,
, 为等腰直角三角形,
为等腰直角三角形, ,且
,且 分别是
分别是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
(3)若点 是
是 上一点,求
上一点,求 的最小值.
的最小值.
设有关于 的一元二次方程
的一元二次方程 .
.
(1)若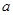 是从
是从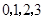 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若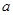 是从区间
是从区间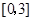 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
已知函数 (其中
(其中 ),
), .
.
(1)若命题
 是假命题,求
是假命题,求 的取值范围;
的取值范围;
(2)若命题 ,命题
,命题
 满足
满足 或
或 为真命题,若
为真命题,若 是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围.
的取值范围.
在 中,
中, 分别为内角
分别为内角 的对边,且
的对边,且 .
.
(1)求角 的大小;
的大小;
(2)设函数 ,当
,当 =
= 时,判断
时,判断 的形状.
的形状.