如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点,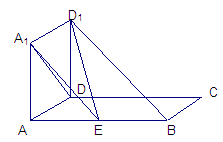
(1).求证:D1E⊥A1D;
(2).在线段AB上是否存在点M,使二面角D1-MC-D的大小为 ?,若存在,求出AM的长,若不存在,说明理由
?,若存在,求出AM的长,若不存在,说明理由
已知数列{an}满足a1="3" , (
( ),数列{bn}满足
),数列{bn}满足 .
.
(1)证明数列{bn}是等差数列并求数列{bn}的通项公式;
(2)求数列{a n}的前n项和S n.
已知函数 的图象过点
的图象过点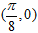 .
.
(1)求实数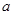 的值;
的值;
(2)求函数f(x)的最小正周期及最大值.
(本小题满分12分)已知函数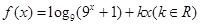 为偶函数.
为偶函数.
(1)求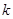 的值;
的值;
(2)解关于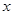 的不等式
的不等式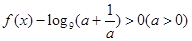
(本小题满分12分)已知首项都是1的两个数列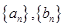 ,
, ,满足
,满足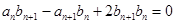 .
.
(1)令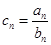 ,求数列
,求数列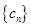 的通项公式;
的通项公式;
(2)若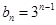 ,求数列
,求数列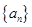 的前n项和
的前n项和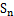
(本小题满分12分)已知函数 -
-
(1)求 的最小正周期及其对称中心;
的最小正周期及其对称中心;
(2)如果三角形ABC的三边a、b、c满足b2=ac,且边b所对角为x,试求x的范围及此时函数 的值域.
的值域.