在数学趣味知识培训活动中,甲乙两名学生的5次培训成绩如茎叶图所示: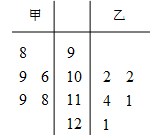
(1)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(2)从乙的5次培训成绩中随机选择2个,试求选到121分的概率.
在等差数列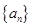 中,
中,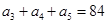 ,
,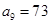 .
.
(1)求数列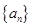 的通项公式;
的通项公式;
(2)对任意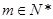 ,将数列
,将数列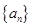 中落入区间
中落入区间 内的项的个数记为
内的项的个数记为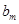 ,求数列
,求数列 的前
的前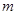 项和
项和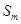 .
.
已知定义域为R的函数f(x)= 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
已知函数f(x)对任意x、y∈R都有f(x+y)=f(x)+f(y),且x>0时,f(x)<0,f(1)=-2.
(1)判断函数f(x)的奇偶性.
(2)当x∈[-3,3]时,函数f(x)是否有最值?如果有,求出最值;如果没有,请说明理由.
若f(x)=x2+bx+c,且f(1)=0,f(3)=0.
(1)求b与c的值;
(2)试证明函数y=f(x)在区间(2,+∞)上是增函数.