如图1,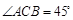 ,
,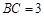 ,过动点A作
,过动点A作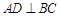 ,垂足D在线段BC上且异于点B,连接AB,沿
,垂足D在线段BC上且异于点B,连接AB,沿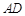 将△
将△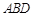 折起,使
折起,使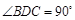 (如图2所示).
(如图2所示).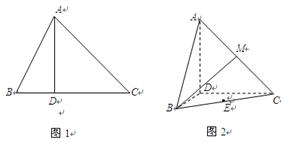
(1)当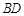 的长为多少时,三棱锥
的长为多少时,三棱锥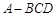 的体积最大;
的体积最大;
(2)当三棱锥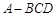 的体积最大时,设点
的体积最大时,设点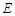 ,
,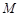 分别为棱
分别为棱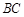 ,
,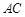 的中点,试在棱
的中点,试在棱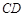 上确定一点
上确定一点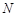 ,使得
,使得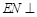
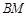 ,并求
,并求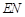 与平面
与平面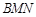 所成角的大小.
所成角的大小.
已知定义在实数集R上的函数y=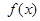 满足条件:对于任意实数x、y都有f(x+y)=f(x)+f(y).(1)求f(0);(2) 求证:
满足条件:对于任意实数x、y都有f(x+y)=f(x)+f(y).(1)求f(0);(2) 求证: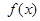 是奇函数;(3) 若
是奇函数;(3) 若 时,
时, ,求
,求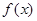 在
在 上的值域.
上的值域.
已知函数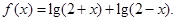
(1)求函数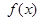 的定义域;
的定义域;
(2)记函数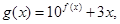 求函数
求函数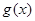 的值域.
的值域.
某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为 ,则出厂价相应提高的比例为
,则出厂价相应提高的比例为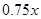 ,同时预计年销售量增加的比例为
,同时预计年销售量增加的比例为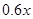 .已知年利润=(出厂价–投入成本)
.已知年利润=(出厂价–投入成本)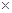 年销售量.
年销售量.
(1)写出本年度预计的年利润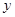 与投入成本增加的比例
与投入成本增加的比例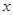 的关系式;
的关系式;
(2)为使本年度的年利润比上年有所增加,问投入成本增加的比例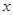 应在什么范围内?
应在什么范围内?
设全集为R,集合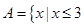 或
或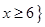 ,
,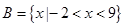 .
.
(1)求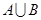 ,
,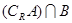 ;
;
(2)已知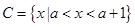 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数f(x)=x2+2ax+2,x∈[-5,5].
(1)当a=-1时,求函数f(x)的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在[-5,5]上是单调增函数.