设 .
.
(1)在下列直角坐标系中画出 的图像;
的图像;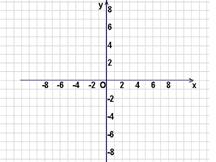
(2)若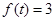 ,求
,求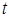 值;
值;
(3)用单调性定义证明函数 在
在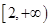 时单调递增.
时单调递增.
已知函数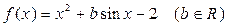 ,
, 且
且 是偶函数.
是偶函数.
(1)求函数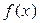 的解析式;
的解析式;
(2)已知函数 在区间
在区间 上单调,
上单调,
求实数 的取值范围.
的取值范围.
已知数列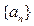 是首项为1的等差数列,其公差
是首项为1的等差数列,其公差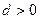 ,且
,且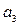 ,
,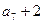 ,
,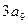 成等比数列.
成等比数列.
(1)求数列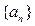 的通项公式;
的通项公式;
(2)设数列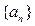 的前n项和为
的前n项和为 ,求
,求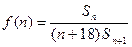 的最大值.
的最大值.
已知函数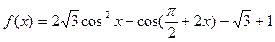
(1)求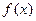 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若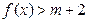 在
在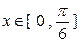 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
已知 为
为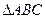 的三个内角,且其对边分别为
的三个内角,且其对边分别为 ,且
,且 .
.
(1)求角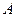 的值;
的值;
|
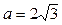 ,
, ,求
,求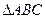 的面积.
的面积.
(本小题满分12分)过椭圆 引两条切线PA、PB、A、B为切点,如直线AB与x轴、y轴交于M、N两点.
引两条切线PA、PB、A、B为切点,如直线AB与x轴、y轴交于M、N两点.
(1)若 ,求P点坐标;
,求P点坐标;
(2)求直线AB的方程(用 表示);
表示);
(3)求△MON面积的最小值.(O为原点)