对有线性相关关系的两个变量建立的线性回归方程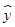
＝
＋
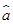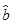x，关于回归系数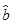，下面叙述正确的是________．
①可以小于0；②大于0；③能等于0；④只能小于0.
若集合A=
，B=
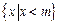满足A∪B=R，A∩B=
，则实数m=" ▲" ．
（本小题满分12分）
已知函数f（x）＝ln（x＋a）－x2－x在x＝0处取得极值．
（Ⅰ）求实数a的值；
（Ⅱ）若关于x的方程f（x）＝－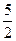
x＋b在区间[0，2]上恰有两个不同的实数根，求实数b的取值范围；
（Ⅲ）证明：对任意的正整数n，不等式ln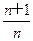
<
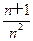都成立．
（本小题满分12分）
已知抛物线y2＝mx的焦点到准线距离为1，且抛物线开口向右．
（Ⅰ）求m的值；
（Ⅱ）P是抛物线y2＝mx上的动点，点B，C在y轴上，圆（x－1）2＋y2＝1内切于
△PBC，求△PBC面积的最小值．
（本小题满分12分）
数列{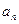
}，{
}，{
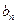}满足a0＝1，b0＝1，c0＝0，且＝
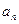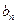＋2，＝2
，＝
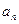
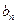＋，n∈N﹡．
（Ⅰ）求数列{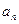}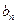，{}的通项公式；
（Ⅱ）求使>7000的最小的n的值．
（本小题满分12分）
某单位有三辆汽车参加某种事故保险，年初向保险公司缴纳每辆900元的保险金，对在一年内发生此种事故的每辆汽车，单位可获9000元的赔偿（假设每辆车每年最多只赔偿一次），设这三辆车在一年内发生此种事故的概率分别为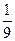
、
、
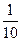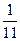，且各车是否发生事故相互独立，求一年内该单位在此保险中：
（Ⅰ）获赔的概率；
（Ⅱ）获赔金额ξ的分布列与期望．