想象一下一个人从出生到死亡,在每个生日都测量身高,并作出这些数据的散点图,这些点将不会落在一条直线上,但在一段时间内的增长数据有时可以用线性回归来分析,下表是一位母亲给儿子做的成长记录:
| 年龄/周岁 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 身高/cm |
91.8 |
97.6 |
104.2 |
110.9 |
115.6 |
122.0 |
128.5 |
| |
|||||||
| 年龄/周岁 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| 身高/cm |
134.2 |
140.8 |
147.6 |
154.2 |
160.9 |
167.5 |
173.0 |
(1)年龄(解释变量)和身高(预报变量)之间具有怎样的相关关系?
(2)如果年龄相差5岁,则身高有多大差异(3~16岁之间)?
(3)如果身高相差20 cm,其年龄相差多少(3~16岁之间)?
(4)计算残差,说明该函数模型是否能够较好地反映年龄与身高的关系,说明理由.
(本小题满分10分)已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图是一个底边长为6,高为4的等腰三角形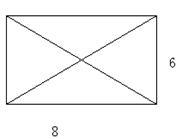
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
(本小题满分10分)
设
(1)求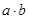 的最大值;
的最大值;
(2)求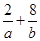 最小值.
最小值.
数列 的首项为
的首项为 ,前n项和为
,前n项和为 ,且
,且 ,设
,设 ,cn=k+b1+b2+…+bn(k∈R+).
,cn=k+b1+b2+…+bn(k∈R+).
(1)求数列{an}的通项公式;
(2)当t=1时,若对任意n∈N*,|bn|≥|b3|恒成立,求a的取值范围;
(3)当t≠1时,试求三个正数a,t,k的一组值,使得{cn}为等比数列,且a,t,k成等差数列.
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).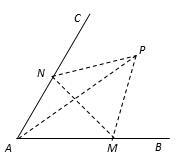
已知数列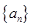 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且
(1)数列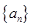 的通项公式;
的通项公式;
(2)设数列 满足
满足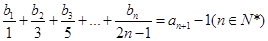 ,求该数列
,求该数列 的前n项和
的前n项和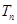 .
.