甲、乙两位篮球运动员进行定点投蓝,每人各投4个球,甲投篮命中的概率为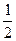 ,乙投篮命中的概率为
,乙投篮命中的概率为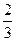 .
.
(1)求甲至多命中2个且乙至少命中2个的概率;
(2)若规定每投篮一次命中得3分,未命中得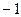 分,求乙所得分数
分,求乙所得分数 的概率分布和数学期望.
的概率分布和数学期望.
某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路(如图所示).在点A与圆弧上的一点C之间设计为直线段小路,在路的两侧边缘种植绿化带;从点C到点B设计为沿弧BC的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)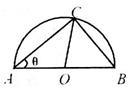
(Ⅰ)设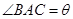 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为 的函数
的函数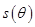 ;
;
(Ⅱ)试确定 的值,使得绿化带总长度最大.
的值,使得绿化带总长度最大.
已知数列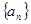 的前
的前 项和为
项和为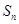 ,且
,且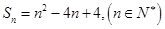
(1)求数列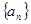 的通项公式;
的通项公式;
(2)数列 中,令
中,令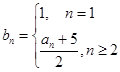 ,
, 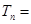
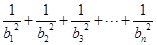 ,求证:
,求证: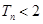 .
.
如图,在四棱柱 中,侧面
中,侧面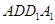 ⊥底面
⊥底面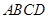 ,
,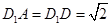 ,底面
,底面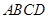 为直角梯形,其中
为直角梯形,其中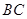 ∥
∥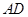 ,
,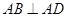 ,
,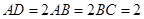 ,
, 为
为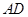 中点.
中点.
(1)求证: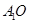 ∥平面
∥平面 ;
;
(2)求锐二面角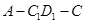 的余弦值.
的余弦值.
用数学归纳法证明:
已知函数 .
.
(Ⅰ)求函数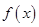 的单调递减区间;
的单调递减区间;
(Ⅱ)设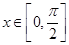 时,函数
时,函数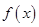 的最小值是
的最小值是 ,求
,求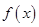 的最大值.
的最大值.