先化简再求值: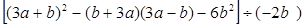 其中
其中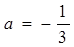 ,
,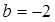
如图,⊙O的直径AB=6cm,P是AB延长线上的一点,过点P作⊙O的切线,切点为C,连接AC,BC.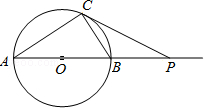
(1)若∠CPA=30°,求PC的长;
(2)探究:当点P在AB的延长线上运动时,是否总存在∠PCB=∠CAB?若存在,请证明;若不存在,请说明理由.
如图,方格纸中的每个小方格都是边长为1个单位的小正方形,每个小正方形的顶点称为格点.△ABC的顶点都在格点上,建立平面直角坐标系后,点A,B,C的坐标分别为(1,1),(4,2),(2,3).
(1)画出△ABC向左平移4个单位,再向上平移1个单位后得到的△A1B1C1;
(2)画出△ABC关于原点O对称的△A2B2C2;
(3)以点A,A1,A2为顶点的三角形的面积为 .
元旦期间,某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得_________元购物券,最多可得_________元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
先化简,再求值: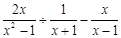 ,其中
,其中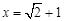 .
.
(1)计算: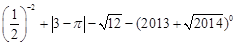 ;
;
(2)解方程: .
.