已知等差数列 的前
的前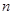 项和为
项和为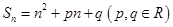 ,且
,且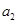 、
、
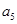 成等比数列.
成等比数列.
(1)求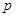 、
、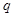 的值;
的值;
(2)若数列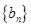 满足
满足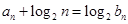 ,求数列
,求数列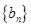 的前
的前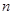 项和
项和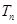 .
.
已知函数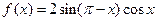 .
.求
 的最小正周期;
的最小正周期;求
 在区间
在区间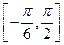 上的最大值和最小值.
上的最大值和最小值.
已知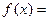
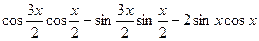 ,当
,当 ,求函数
,求函数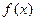 的零点.
的零点.
对于函数y=f(x),若x1+x2="1," 则f(x1)+f(x2)=1,记数列f(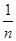 ),f(
),f( ),
),
……,f( )……,(n≥2,n∈
)……,(n≥2,n∈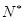 )的前n项的和为Sn ;
)的前n项的和为Sn ;
(1)求Sn;
(2)若a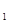 =
=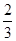 ,a
,a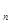 =""
="" 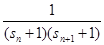 (n≥2,n∈
(n≥2,n∈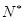 ),
),
对于函数y=f(x),若x1+x2="1," 则f(x1)+f(x2)=1,记数列f(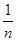 ),f(
),f(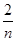 ),
),
……,f(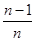 )……,(n≥2,n∈
)……,(n≥2,n∈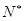 )的前n项的和为Sn ;
)的前n项的和为Sn ;
(1)求Sn;
(2)若a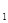 =
=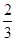 ,a
,a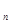 =""
="" 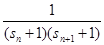 (n≥2,n∈
(n≥2,n∈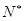 ),
),
右面的图形无限向内延续,最外面的正方形的边长等1。从外到内,第i个正方形与内切圆之间的深灰色图形面积记为Si(i="1," 2, …)。
分别求S1,S2,Sk;
求深灰色图形的面积的总和。