某中学将 名高一新生分成水平相同的甲、乙两个“平行班”,每班
名高一新生分成水平相同的甲、乙两个“平行班”,每班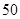 人,吴老师采用
人,吴老师采用 、
、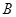 两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取
两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取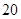 名学生的成绩进行统计,作出的茎叶图如下:
名学生的成绩进行统计,作出的茎叶图如下: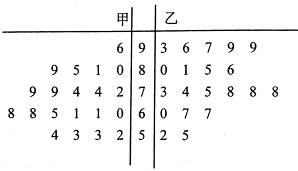
记成绩不低于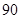 分者为“成绩优秀”.
分者为“成绩优秀”.
(1)在乙班样本的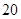 个个体中,从不低于
个个体中,从不低于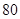 分的成绩中随机抽取
分的成绩中随机抽取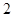 个,记随机变量
个,记随机变量 为抽到“成绩优秀”的个数,求
为抽到“成绩优秀”的个数,求 的分布列及数学期望
的分布列及数学期望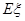 ;
;
(2)由以上统计数据填写下面 列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
| |
甲班( 方式) 方式) |
乙班(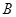 方式) 方式) |
总计 |
| 成绩优秀 |
|
|
|
| 成绩不优秀 |
|
|
|
| 总计 |
|
|
|
已知集合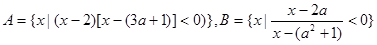 .
.
(1)当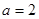 时,求
时,求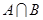 ;
;
(2)求使 的实数
的实数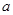 的取值范围.
的取值范围.
已知z为复数,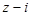 和
和 均为实数,其中
均为实数,其中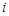 是虚数单位.
是虚数单位.
(1)求复数z;
(2)若复数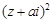 在复平面上对应的点在第一象限,求实数a的取值范围.
在复平面上对应的点在第一象限,求实数a的取值范围.
(1)已知函数f(x)=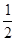 x
x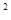 -ax+(a-1)
-ax+(a-1)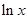 ,
,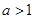 。讨论函数
。讨论函数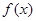 的单调性;
的单调性;
(2).已知函数f (x)=lnx,g(x)=ex.设直线l为函数 y=f (x) 的图象上一点A(x0,f (x0))处的切线.问在区间(1,+∞)上是否存在x0,使得直线l与曲线y=g(x)也相切.若存在,这样的x0有几个?,若没有,则说明理由。
如图,己知平行四边形ABCD中,∠ BAD = 600,AB=6, AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG。
(I)求证:直线CE//平面ABF;
(II)如果FG⊥平面ABCD求二面B一EF一A的平面角的余弦值.
(Ⅲ)若直线AF与平面 ABCD所成角为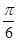 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD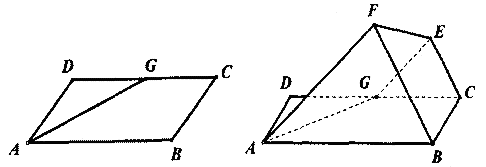
如图,一个小球从M处投入,通过管道自上而下落A或B或C。已知小球从每个叉口落入左右两个 管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,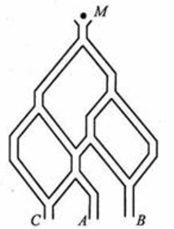
2,3等奖.(I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量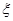 为获得k(k=1,2,3)等奖的折扣率,求随机变量
为获得k(k=1,2,3)等奖的折扣率,求随机变量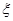 的分布列及期望
的分布列及期望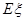 ;(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量
;(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量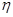 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求 .
.