 .
.
(本题满分14分)已知函数 .
.
(1)求函数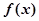 的单调区间;
的单调区间;
(2)若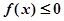 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(文科(3)证明: 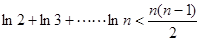
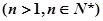 .
.
(理科(3)证明: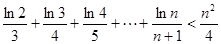
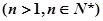 .
.
(本题满分12分)已知椭圆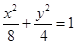 ,过中心O作互相垂直的线段OA、OB与椭圆交于A、B, 求:
,过中心O作互相垂直的线段OA、OB与椭圆交于A、B, 求:
(1)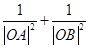 的值
的值
(2)判定直线AB与圆 的位置关系
的位置关系
(文科)(3)求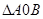 面积的最小值
面积的最小值
(理科)(3)求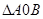 面积的最大值
面积的最大值
设函数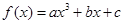
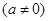 为奇函数,其图象在点
为奇函数,其图象在点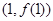 处的切线与直线
处的切线与直线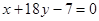 垂直,导函数
垂直,导函数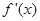 的最小值为
的最小值为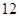 .
.
(1)求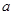 ,
,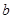 ,
,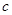 的值;
的值;
(2)若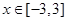 时,
时,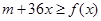 恒成立,求
恒成立,求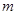 的范围;
的范围;
(3)设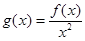 ,当
,当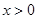 时,求
时,求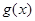 的最小值.
的最小值.
本题满分12分)已知直线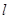 的参数方程为:
的参数方程为: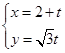 (t为参数),曲线C的极坐标方程为:
(t为参数),曲线C的极坐标方程为: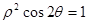 .
.
(1)求直线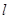 被曲线C截得的弦长,
被曲线C截得的弦长,
(2)若直线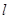 与曲线C交于A、B两点,求线段AB的中点坐标.
与曲线C交于A、B两点,求线段AB的中点坐标.
设命题p:函数 是R上的减函数,命题q:函数f(x)=x2-4x+3在
是R上的减函数,命题q:函数f(x)=x2-4x+3在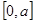 上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求
上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求 的取值范围.
的取值范围.