求与直线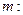
 平行且距离等于
平行且距离等于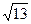 的直线
的直线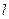 方程.
方程.
)已知定义域为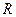 的两个函数
的两个函数 ,对于任意的
,对于任意的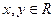 满足:
满足: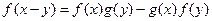 且
且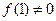
(Ⅰ)求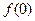 的值并分别写出一个
的值并分别写出一个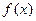 和
和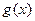 的解析式,使它们满足已知条件(不要求说明理由)
的解析式,使它们满足已知条件(不要求说明理由)
(Ⅱ)证明: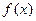 是奇函数;
是奇函数;
(Ⅲ)若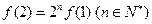 ,记
,记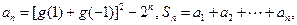
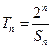 ,求证:
,求证: 
已知 、
、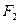 分别是椭圆C:
分别是椭圆C: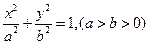 的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过
的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过 的弦
的弦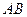 两端点
两端点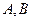 与
与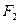 所成⊿
所成⊿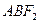 的周长是
的周长是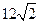 .
.
(Ⅰ).求椭圆C的标准方程.
(Ⅱ)已知点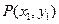 ,
,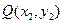 是椭圆C上不同的两点,线段
是椭圆C上不同的两点,线段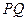 的中点为
的中点为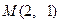 .
.
求直线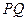 的方程;
的方程;
(Ⅲ)若线段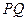 的垂直平分线与椭圆C交于点
的垂直平分线与椭圆C交于点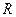 、
、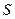 ,试问四点
,试问四点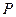 、
、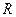 、
、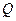 、
、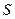 是否在同一个圆上,若是,求出该圆的方程;若不是,请说明理由.
是否在同一个圆上,若是,求出该圆的方程;若不是,请说明理由.
如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=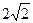 .
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P—CD—B的大小;
(Ⅲ)求点C到平面PBD的距离. 
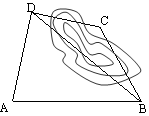
如图,为了计算北江岸边两景点 与
与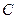 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和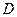 两个测量点,现测得
两个测量点,现测得 ,
, ,
, ,
,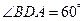 ,
,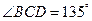 ,求两景点
,求两景点 与
与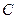 的距离(假设
的距离(假设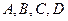 在同一平面内,测量结果保留整数;参考数据:
在同一平面内,测量结果保留整数;参考数据: )
)