学生的数学学习水平按成绩可分成8个等级，等级系数X依次为1，2， ，8，其中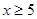
为标准A，
为标准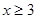B.已知甲学校执行标准A考评学生，学生平均用于数学的学习时间为3.5小时/天；乙学校执行标准B考评学生，学生平均用于数学的学习时间为2.5小时/天.假定甲、乙两学校都符合相应的执行标准.
（1）已知甲学校学生的数学学习水平的等级系数X1的概率分布列如下所示：
| X1 |
5 |
6 |
7 |
8 |
| P |
0.4 |
a |
b |
0.1 |
且X1的数学期望EX1=6，求a、b的值；
（2）为分析乙学校学生的数学学习水平的等级系数X2，从该校随机选取了30名学生，相应的等级系数组成一个样本，数据如下：
3533855634
6347534853
8343447567
用这个样本的频率分布估计总体分布，将频率视为概率，求等级系数X2的数学期望；
（3）在（1）、（2）的条件下，哪个学校的数学学习效率更高？说明理由.
(注：
)
，集合
，
．
；
．
为奇函数，
为偶函数，且
．
上是减函数；
的方程
有解，求实数
的取值范围．
．
是奇函数，求
与
的值；
的解集
，求实数
的取值范围；
，求实数
的取值集合．
，求函数
的最大值和最小值．