一绝缘“U”型杆由两段相互平行的足够长的竖直直杆PQ、MN和一半径为R的光滑半圆环QAN组成.固定在竖直平面内，其中杆PQ是光滑的，杆MN是粗糙的，整个装置处在水平向右的匀强电池中.在QN连线下方区域足够大的范围内同时存在垂直竖直平面向外的匀强磁场，磁感应强度为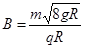
.现将一质量为m、带电量为-q（q＞0）的小环套在PQ杆上，小环所受的电场力大小为其重力的3倍.（重力加速度为g）.求：
（1）若将小环由C点静止释放，刚好能达到N点，求CQ间的距离；
（2）在满足（1）问的条件下，小环第一次通过最低点A时受到圆环的支持力的大小；
（3）若将小环由距Q点8R处静止释放，设小环与MN杆间的动摩擦因数为u，小环所受最大静摩擦力大小相等，求小环在整个运动过程则克服摩擦力所做的功.
如图所示，A、B两物体的质量都为m，拉A物体的细线与水平方向的夹角为30°时处于静止状态，不考虑摩擦力，设弹簧的劲度系数为k。若将悬线突然剪断，A在水平面上做周期为T的简谐运动，当B落地时，A恰好将弹簧压缩到最短，求：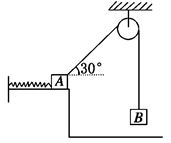
(1)A振动时的振幅；
(2)B落地时的速度．
有一台发电机通过升压和降压变压器给用户供电，已知发电机的输出功率是20kW，端电压为400V，升压变压器原、副线圈的匝数比为n1﹕n2=1﹕5，两变压器之间输电导线的总电阻R=l.0Ω，降压变压器输出电压U4＝220V，求：
（1）升压变压器的输出电压；
（2）输电线路输送电能的效率多大；
（3）降压变压器的原、副线圈的匝数比n3﹕n4；
如图10所示，MN、PQ是两条水平放置的平行光滑导轨，其阻值可以忽略不计，轨道间距L=0.6m。匀强磁场垂直导轨平面向下，磁感应强度B=1.0×10
T，金属杆ab垂直于导轨放置与导轨接触良好，ab杆在导轨间部分的电阻r=1.0Ω,在导轨的左侧连接有电阻R1、R2,阻值分别为R1="3.0Ω," R2 =6.0Ω,ab杆在外力作用下以v=5.0m/s的速度向右匀速运动。
（1）ab杆哪端的电势高？
（2）求通过ab杆的电流I。
如图3-2所示。在有明显边界PQ的匀强磁场B外有一个与磁场垂直的正方形闭合线框其电阻为R。用一个平行线框的力将此线框匀速地拉进磁场。设第一次速度为v，第二次速度为2 v，求两次拉力大小之比多少？
在火箭内的平台上放有测试仪器，火箭从地面启动后，以加速度g/2竖直加速上升，升到某一高度时，测试仪对平台的压力为启动前压力的17/18，已知地球半径R = 6.4×106 m。求火箭此时离地面的高度为多少？