如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.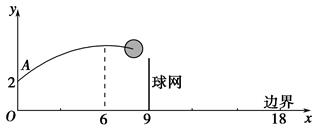
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
如图所示,已知圆锥底面半径r=10cm,母线长为40cm.求它的侧面展开图的圆心角和表面积.
若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?

小红和小慧玩纸牌游戏.如图是同一副扑克中的4张牌的正面,将它们正面朝下洗匀后放在桌上,小红先从中抽出一张,小慧从剩余的3张牌中也抽出一张. 请用树状图表示出两人抽牌可能出现的所有结果;
求抽出的两张牌都是偶数的概率.

如图,P为等边△ABC的中心.画出将△ABP绕A逆时针旋转60°的图形;(不写画法,保留作图痕迹)
经过什么样的图形变换,可以把△ABP变换到右边的△CMN,请写出简要的文字说明.
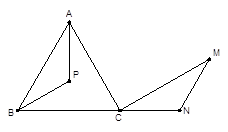
如图,在△ABC中,∠ B=90°,AB=6cm,BC=8cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.
如果P、Q分别从A、B同时出发,经过多长时间,使△PBQ的面积为8cm2?
如果P、Q分别从A、B同时出发, 当P、Q两点运动几秒时,
 有最小值,并求这个最小值.
有最小值,并求这个最小值.
如图所示, 是直角三角形,
是直角三角形, ,以
,以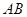 为直径的⊙O交
为直径的⊙O交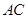 于点
于点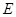 ,点
,点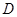 是
是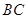 边的中点,连结
边的中点,连结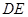 .
.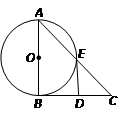
求证:
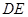 与⊙O相切
与⊙O相切若⊙O的半径为
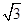 ,
,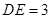 ,求
,求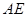 .
.